Jul 11 2012
Metrics in Lean – Part 5 – Lead times and inventory
As in the article on Nike, Lead time reduction is often touted as Lean’s greatest achievement. Improvements in productivity, quality and new product introduction time make it into the first paragraph, but lead times get the headline. Lead time metrics are popular, but there are many different lead times that are of interest and they are not easy to define, measure, or interpret. Inventory is easier to measure and, under stable conditions, Little’s Law provides some information about average lead times, details on lead time distributions can be inferred from inventory age statistics. In addition, inventory metrics are useful in their own right, to support improvements in storage and retrieval, materials handling, and supply chain management.
- What do we call a lead time?
- Measuring lead times directly
- Average lead times add up, extreme values don’t
- Interpretation and use
- Theoretical versus actual lead time
- “Days of inventory” and Little’s Law
- Inventory, throughput, and average lead times
- Inventory, Inventory age analysis and lead time distribution
- Inventory metrics
Contents
- What do we call a lead time?
- Measuring lead times directly
- Average lead times add up, extreme values don’t
- Interpretation and use
- Theoretical versus actual lead time
- “Days of inventory” and Little’s Law
- Inventory, throughput, and average lead times
- Inventory age analysis and lead time distribution
- Inventory metrics
What do we call a lead time?
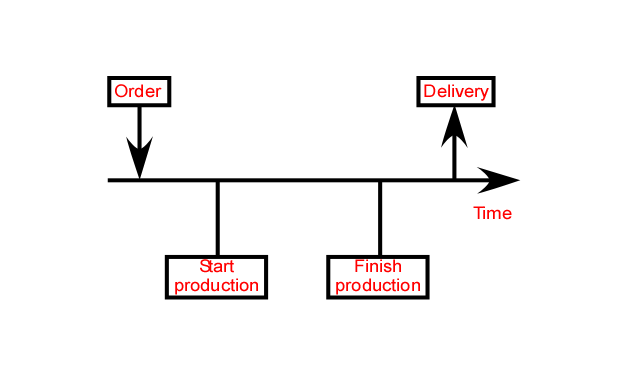
In its most general form, the lead time of an object through a system is the interval between the time it enters the system and the time it leaves it. The objects can be material, like manufacturing work pieces, or data, like a passport application, or a combination of both, like a pull signal or a customer order for a manufactured product, which starts as data and ends as materials accompanied with delivery documents. The system is any part of your business that you can draw a boundary around and monitor objects going in and coming out.
Order fulfillment lead time is, in principle, well defined as the interval between the placement of the order and receipt of the goods by the customer. The objects are orders and the system is comprised of your own company and its distribution network. There is no ambiguity as to the time the order is placed when a consumer confirms the checkout for an on-line cart, nor is there about the time of delivery when it is recorded by the delivery service. On the other hand, business-to-business transactions frequently do not have that clarity, particularly on large, long-term orders. If a customer places an order for 12 monthly deliveries, strictly speaking, the order fulfillment lead time is one year, which is not terribly useful. Then you have to identify a trigger point to start the clock for each delivery. If you use Kanbans or other types of pull signals, they can be used for this purpose.
Inside the company, if production work is organized in jobs or work orders, you can measure the time between release by production control and completion, and that gives you an internal, manufacturing lead time. If you produce the same item every day one piece at a time, you can record the times through a production line by serial number. But the existence of scrap and rework makes this a bit more complicated. The parts that do not make it out of the line tie up capacity and slow down the others, and the parts that are reworked undergo extra processing, adding to the lead time and increasing its variability. When calculating lead times for a process, however, you should only consider the units that make it out as good product.
An assembly process involves multiple flows merging. It is somewhat like a river basin, and there is often no objective criterion for deciding which of two merging rivers is the main stream and which one the tributary. Usually, the smaller river is designated as the tributary, but there are exceptions. By this criterion, for example, the river crossing Paris should be called the Yonne rather than the Seine, because, as French kids learn in primary school, where they merge upstream from Paris, the Yonne is the larger of the two (See Figure 1).
Figure 1. A tributary larger than the mainstream
Likewise, in assembly, working upstream from the end, you have to decide which flow is the main and which are feeder lines. It is a simple call where you are mounting a side rear-view mirror on a car, but less obvious when you are mating an engine and transmission assembly with a painted body.
Measuring lead times directly
Tracing the lead time of completed units through multiple operations requires a history database with timestamps for all the relevant boundary crossings. This is only available if there is a tracking system collecting this data. If the data collection is manual, it often occurs at the end of each shift, meaning that we know in which shift the event occurred but not at what time within that shift, as shown in Figure 2. To measure lead times in weeks, it is accurate enough; in hours, it isn’t.
Figure 2. Operators recording production activity at the end of the shift
The direct measurement of lead times is also problematic with rapidly evolving, high-technology processes that have manufacturing lead times in months. If a part goes through 500 operations in 4 months, its actual lead time will commingle data about current conditions at the last operation with four-month-old data about the first one. Since then, three additional machines may have been brought on line, two engineering changes to the process may have taken place, and volume may have doubled, all of which makes the old data useless. It would be more useful to have a snapshot of the lead time under current conditions, with the understanding that it is an abstraction because, as the process keeps evolving, no actual part will ever make it from beginning to end under these exact conditions. To get such a snapshot, we need to measure lead times for individual operations, which raises the question of how we can infer lead times for an entire process from operation lead times.
Average lead times add up, extreme values don’t
When we have lead times for operations performed in sequence, we want to add them up like the times between stations on a train line, to get a lead time for the entire process. For each object flowing through, it always works: the time it needs to go through operations 1 and 2 is the sum of its times through Operation 1 and Operation 2.When we look at populations of objects flowing through, it is a different story. The averages still add up by simple arithmetic. The problem is that the average is usually not what we are interested in. When accepting customer orders, we want to make promises we are sure to keep, which means that our quotes must be based not on lead time averages but on upper-bounds, so that, in the worst-case scenario, we can still deliver on time. We need to be careful, however, because extreme values are not additive. The worst-case scenario for going through operations 1 and 2 is not the sum of the worst-case scenario through Operation 1 and the worst-case scenario through Operation 2.
That it is wrong to add the worst-case times is easiest to see when considering two operations in sequence in a flow line, when variability in the first operation causes you to maintain a buffer between the two. If one part takes especially long through the first operation, then the buffer will be empty by the time it reaches the second and its time through it will be short, and it makes no sense to add the longest possible times for both operations. If it takes you an unusually long time to go through passport control at an airport, your checked luggage will be waiting for you at the carrousel and you won’t have to wait for it. In other words, the times through both operations are not independent.
A job shop is more like a farmer’s market (See Figure 3). At each operation, each waits in line with other parts arriving by different paths, like customers in queues at different stalls in the market. Then the times through each operation are independent, and the extreme values for a sequence of operations can be calculated simply, but not by addition. This is because, for independent random variables, it is the squares of the standard deviations that are additive, and not the standard deviations themselves. If operations 1 and 2 have independent lead times with standard deviations σ1 and σ2, the standard deviation for both in sequence is . If the first operation takes 8±2 hours and the second one 5±1 hours, the sequence of the two will take 13 ± 2.2 hours and not 13 ± 3 hours as would be obtained by just adding the extreme values. It is like the hypotenuse of a right triangle versus the sum of its two other sides. Of course, the more operations “standard lead times” you add in this fashion, the worse the lead time inflation. For details on this phenomenon, see Measuring Delivery Performance: A Case Study from the Semiconductor Industry, by J. Michael Harrison et al. in Measures for Manufacturing Excellence, pp.309-351.
Figure 3. A farmers’ market and a machining job shop
Interpretation and use
Process lead times look like task durations in a project, and it is tempting to load them in a program like Microsoft project and treat operations like tasks with finish-to-start constraints and use the project planning and management tools to perform calculations on the production process. Unless you are building a one-of-a-kind prototype or a rarely ordered product, however, manufacturing a product is not a project but an activity involving flow. As a consequence, order fulfillment lead times are usually much shorter than process lead times. You can order a configured-to-order computer on-line and get it delivered within 3 to 5 days, but the processor in it takes months to make. When a manufacturer explains that the business is purely “make-to-order,” it doesn’t usually mean starting by digging for iron ore to make a car. The game is to decide where in the process to start and how to have just the materials you need when you need them, in order to fill customer orders promptly without hoarding inventory.
Lean manufacturers achieve short lead times indirectly by doing the following:
- Engineering production operations for stability and integration into one-piece flow lines. This is never achieved 100% but is always pursued.
- Designating your products as runners, repeaters or strangers, and lay out production lines and logistics differently for each category.
- In mixed-flow lines, applying SMED to reduce changeover times.
- Applying leveled-sequencing (heijunka) as needed in scheduling production lines.
- Using a pull system to manage both in-plant and supply-chain logistics.
In an existing factory, the challenge of reducing lead times is often mistakenly perceived as involving only production control and supply chain management in actions limited to production planning, production scheduling, and materials procurement. Because materials in the factory spend so little of their time being worked on, improving production lines is viewed at best as secondary, and at worst as a waste of time, because “production already been optimized.” In reality, it is nothing of the kind, and one key reason materials wait so long is dysfunctional production. Improve the productivity and flexibility of manufacturing operations, lay out your lines to make it easiest to do what you do the most often, and you see the waiting times melt away, creating the opportunity to use more sophisticated methods in support of production. This perspective is a key difference between Lean Manufacturing and the theory of constraints or the approaches proposed in the academic literature on operations management, such as Factory Physics.
Theoretical versus actual lead time
In analyzing lead times, we separate the time the object spends waiting from the time it is being worked on, making progress towards completion. This serves two purposes:
- Establishing the lower limit of lead time under current process conditions. The fastest the object can move through the system is if it never waited.
- Understanding the ratio of working to waiting, and making it a target for improvement.
The dual timelines at the bottom of a Value Stream Map bear lead time and process time data. The sum of these process time data is often called theoretical lead time or theoretical cycle time, after which actual performance is often described as “We’re running at five times theoretical…” How exactly the theoretical lead time is calculated is usually not specified.
What I recommend to calculate a meaningful theoretical lead time for a product is a thought experiment based on the following assumptions:
- The plant has no work to do, except except making one piece of the product.
- The following is ready and available for this one piece:
- Materials
- Equipment.
- Jigs, fixtures, and tools
- Data, like process programs or build manifests.
- Operators.
- Transportation between operations is instantaneous.
- There is no inspection or testing, except where documented results are part of the product, as is common in aerospace or defense.
Under these conditions, the theoretical lead time is what it would take to make the unit from start to finish. These assumptions have the following consequences:
- Since we assume the equipment is ready, no setup time is involved.
- The process time through an operation involving a machine includes loading and unloading.
- If a machine processes a load of parts simultaneously, the processing time for a single part is the same as for a load. If an oven cures 100 parts simultaneously in two hours, it still takes two hours to cure just one part.
On the other hand, there are cases for which our assumptions still leave some ambiguity. Take, for example, a moving assembly line with 50 stations operating at a takt time of 1 minute. If we treat it as one single operation, our product unit will take 50 minutes to cross it from the first station to the last. On the other hand, to make just one part, the line does not have to move as a constant pace. The amount of assembly work at each station has to be under 1 minute, and the part transferred to the next station as soon as this work is done, with the result that it takes less than 50 minutes to go through the whole line. You can make an argument for both methods, and the assumptions are not sufficiently specific to make you choose one over the other. What is important here is that the choice be explicit and documented.
The difference between the actual and theoretical lead times can then be viewed as gold in the mine, to be extracted by improvements in all aspects of operations except the actual processes. If you find a way to mill a part twice as fast, you change the theoretical lead time itself. Because the theoretical lead time is usually a small fraction of the actual lead time, say, 5 hours versus 2 months, managers often assume that it makes no sense to focus on finding ways to reduce these 5 hours to 4, and that they should instead focus on the time the materials spend waiting. But, as said above, the two are not independent. Faster processing melts away the queues, and reducing the theoretical lead time by 20% may reduce the actual lead time by 50%.
“Days of inventory” and Little’s Law
Inventory levels are often expressed in terms of days of coverage. 200 units in stock, consumed at the rate of 10 units/day, will last 20 days. Therefore, 200 units is equivalent to 20 days of inventory, and this is what the average lead time for one unit will be. This is the method most commonly used to assign durations to “non-value added activities” on Value Stream Maps.
We should not forget, however, that the validity of this number is contingent on consumption. If it doubles, the same number of parts represents 10 days instead of 20. If consumption drops to zero, then the 200 parts will cover the needs forever.
When, on the basis of today’s stock on hand and today’s throughput, a manager declares that it is “20 days of inventory,” it really means one of the two following assertions:
- If we keep producing at the exact same rate, the current stock will be used up in 20 days, which is simple arithmetic.
- If the production rate and available stock fluctuate around the current levels, the item’s lead time from receiving into the warehouse through production will fluctuate around 20 days, by Little’s Law.
In either one of these interpretations, we have an “instantaneous” lead time that is an abstraction, in the sense that no actual part may take 20 days to go through this process, just as a car going 60 mph this second will not necessarily cover 60 miles in the next hour. In the case of a car, we all understand it is just a speedometer reading; for days of inventory, it is easy to draw conclusions from the number that go beyond what it actually supports.
Inventory, throughput, and average lead times
As we have seen, lead times are difficult to measure directly, because it requires you to maintain and retrieve complete histories for units or batches of units. Inventory is easier to measure, because you only need to retrieve data about the present. First, the inventory database is much smaller than the production history databases. Second, because inventory data are used constantly to plan, schedule, and execute production, it is readily accessible and its accuracy is maintained. For similar reasons, throughput data is also easier to access than history and more accurate. As a result, with all the caveats on assumptions and range of applicability, Little’s Law is the easiest way to infer average lead times.
Inventory age analysis and lead time distribution
In some cases, inventory data lets us infer more than just average lead times. Often, the inventory database contains the date and time of arrival into the warehouse by unit, bin, or pallet. If it cannot be retrieved from the database, it is often available directly from the attached paperwork in the warehouse.Then for a relevant set of items, we can plot a histogram of the ages of the parts in the warehouse, which, as a snapshot of its state, may look like Figure 4.
Figure 4. Inventory age snapshot for one item
If there is “always at least 5 days of inventory,” then we can expect no part to leave the warehouse until it is at least 5 days old, and seek an explanation for the short bar at age 3 days. The bar to the right shows outliers, parts that have been passed over in retrieval for being too hard to reach, or possibly have gone through a special quality procedure. In any case, they are an anomaly that needs investigating.
If the warehouse operations are stable in the sense that there is a lead time distribution, then, if we set aside obvious outliers and take the averages of multiple snapshots taken at different times of the day, the week or the month as needed to smooth out the spikes associated with truck deliveries, the chart should converge to a pattern like that of Figure 5.
Figure 5. Average of multiple snapshots with outliers removed
If a unit is 9 days old in the warehouse, it means that its time in the warehouse will be at least 9 days. The drop between the columns for 9 and for 10 days, then represents the parts that stay at least 9 days but less than 10. In other words, in proportion to the whole, it gives the probability that a part will be pulled on its 10th day in the warehouse. Therefore, by differences, the age distribution gives us the complete distribution of the lead times, as shown in Figure 6.
Figure 6. Lead time distribution inferred from inventory age
Admittedly, this approach cannot always be used. Where it can, it gives us detailed information about lead times at a fraction of the cost of directly measuring it. Even where it cannot be used, snapshots of inventory age still provide valuable information, much like the demographers’ populations pyramids, as in Figure 7.
Figure 7. Example of population pyramids
Inventory metrics
To accountants “resource consumption” is synonymous with cost. As discussed in Part 2, for posting on the shop floor, we need metrics that express performance in the language of things. Depending on circumstances, such substitutes may include the amount of work in process used to sustain production, as a measure of the effectiveness of production management and engineering. When it goes down, it is a both a one-time reduction in working capital and a reduction in recurring holding costs. The unit of measure of WIP can be set locally in each work area.
Many companies measure inventory in terms of its dollar value, of the time it would take to consume it, or the turnover frequency. In doing so, they combine measures of the inventory itself with other parameters, such as the values assigned to inventory by Accounting and an assumed throughput rate. These are legitimate derivative metrics and of interest to management, but when you stand next to a rack on the shop floor, you see pallets and bins, not money, days of supply, or turns. The raw inventory data is comprised of quantities on hand by time, and these should also be used as the basis for simple metrics in the language of things, such as the following:
- Number of pallets, bins and units on hand by item. This is what Operations has to work with, regardless of item cost.
- Number of partial containers in store. The presence of “partials” in store is a sign of a mismatch between batch sizes in quantities received and consumed.
- Floor space occupied by inventory. This is of interest because freed up space can be used to increase production.
- Accuracy of inventory data. This is usually measured by the percentage of items for which database records agree with reality, as observed through cycle counting.
As discussed above, inventory is easier to measure than lead time, and much about lead time can be inferred from inventory status, using tools like Little’s Law or age analysis. But it is not the systematic application of formulas to numbers: we need to be careful about underlying assumptions and the extent to which the data supports our conclusions.








July 14, 2012 @ 11:31 am
Michel, My organization is currently forming metrics for all areas of the enterprise. As Director of Information Technology, I am looking for a good source on what metrics other companies are using to measure IT’s contribution to the organization.
Best Regards,
Greg Buckley
July 15, 2012 @ 8:23 am
I wouod check out Douglas Hubbard, author of “How to measure anything.” He has a theory about the economic value of information that you may find useful. He may have some pointers for benchmarks on metrics for the contribution of IT.
August 29, 2013 @ 5:38 am
I like your thoughts here. I am looking for information on Lead Time exposure as a metric for aircraft readiness. As a manufacturer we can only contribute to overall aircraft readiness. Can you explain or point me to a graphic that depicts using lead time exposure as a supply chain health metric for aircraft readiness. Thanks!
July 6, 2015 @ 2:56 am
Excellent article. I offer a couple of ideas to try to get a decent approximation of lead times
All ERP systems I have worked with over the last 25 years have generated work by using shop orders to make parts or assemblies. They record both planned and actual.
Of course the actuals are vulnerable to when the operator “closes out” the W/O but historically it gives you some stake in the ground
And it allows you to record components being made in parallel for an assembly
As an aside its funny how the BOM never features in CI but it is in many respects the key to understanding flow
I find without a “pull” system the CoV of actual to planned is always high