Dec 17 2022
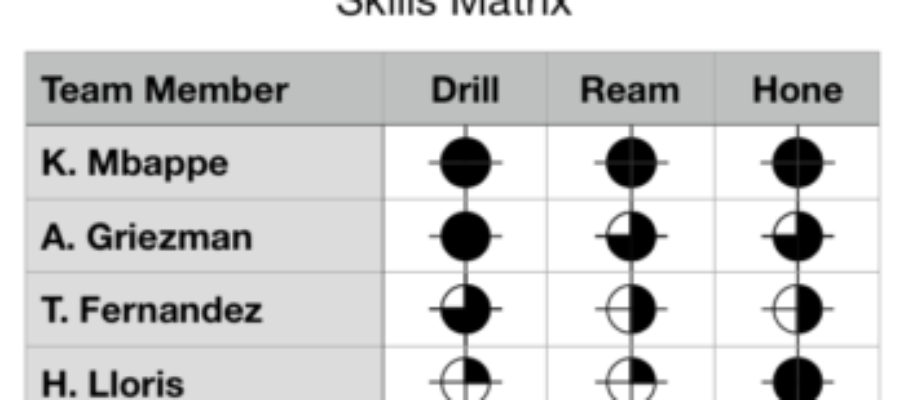
The Skills Matrix
Several sites on the Van of Nerds tour in France in 9/22 maintain skills matrices on the shop floor. It means that the value of the skills matrix is widely known. Several questions must be answered to make it effective:
- The size of the teams represented in one posted matrix.
- The types of skills that should be in the matrix.
- The uses of this tool in daily operations.
- The integration of this tool with Human Resources.




Dec 22 2022
Introduction to Manufacturing — First Print Copies
As co-author of Introduction to Manufacturing, I received the first print copies with trepidation::
For the paperback edition, so far, it’s yes on all counts. Here is a sample of a page spread:
The only elements I found missing are three endorsements of Introduction to Manufacturing that we greatly appreciate:
We hope to see them in the next print run.
#introductiontomanufacturing, #manufacturing
Share this:
Like this:
By Michel Baudin • Announcements 8 • Tags: industrial engineering, Introduction to Manufacturing