Mar 2 2019
The Math Behind The Process Behavior Chart
Ever since asking Is SPC Obsolete? on this blog almost 6 years ago, multiple sources have told me that the XmR chart is a wonderful and currently useful process behavior chart, universally applicable, a data analysis panacea, requiring no assumption on the structure of the monitored variables. So I dug into it and this what I found.
Contents
What’s an XmR chart?
Here is an example of what these charts look like:

The X chart and the mR chart
The top chart shows individual measurements over time; the bottom one, a moving range based on the last two values. What makes this more than a plain times series charts — the likes of which are found in as unsophisticated a publication as USA Today — is the red dashed lines marking control limits.

Misleading time series from USA Today
How control limits are set
The method for setting these limits is essential to the tool.
The Recipe
The limits are multiples of the average of the moving range \overline{mR} . What the literature tells you is that, for the chart of individual values, the limits are at:
Average \pm 2.66\times\overline{mR}
and for the range at
3.27\times\overline{mR}
Concerns about the formulas
The readers are discouraged from worrying their heads with the provenance of these numbers, and the closest they get to an explanation is a reference to a table where such coefficients are kept, and this table was generated by a higher authority. No further explanation is found in the books I have seen by Douglas Montgomery, J.M. Juran, or Don Wheeler.
The assertion that these numbers are valid regardless of the data’s variation pattern strains credulity. Clearly, they did not come out of thin air. There is a theory behind them, that theory is based on assumptions about the data, and it is necessary for users to know these assumptions so that they can understand the domain of applicability of the technique, with its blurry boundaries.
You may still get some use out of the technique when the conditions are not fully met but you should do so knowingly. As discussed in an earlier comment, chemical engineers commonly apply formulas for perfect gases to gases they know aren’t perfect.
The math of limit setting
Not finding this information for the XmR chart, I undertook to work it out myself, starting with the model implicit in the SPC literature, that a process variable X is the sum of a constant C with a white noise W. Formally, for the i-th measurement,
X_{i} = C + W_{i}
where the W_{i} are independent Gaussian (also known as “Normal”) variables with 0 mean and standard deviation σ. Let us consider the differences between consecutive variables X_{i} and X_{i-1}:
X_{i} - X_{i-1} = W_{i} -W_{i-1}
As sums of two independent Gaussian variables with 0 mean and standard deviation σ, they are also Gaussian, with 0 mean and standard deviation \sqrt{2}\times\sigma . The range R_{i} is the absolute value of this difference:
R_{i} = \left |X_{i} - X_{i-1} \right | = \left |W_{i} - W_{i-1} \right |
and follows the Half-Gaussian distribution. The mean \mu_{R} of the range is:
\mu_{R} = \sqrt{\frac{2}{\pi}}\times(\sqrt{2}\sigma) = \frac{2}{\sqrt{\pi}}\times\sigma
and therefore:
\sigma = \frac{\sqrt{\pi}}{2}\times\mu_{R} = 0.8862 \times\mu_{R}
which results in:
3\sigma = 2.66\times\mu_{R}
For the standard deviation \sigma_{R} of the moving range, we have:
\sigma_{R}^{2 }= 2\sigma^{2} -\mu_{R}^{2} = \mu_{R}^{2}\times(\frac{\pi}{2} -1)
This means that, for R, the r\sigma_{R} upper control limit is:
\mu_{R} + 3\sigma_{R} = \mu_{R}\times\left (1 + 3\times\sqrt{\frac{\pi}{2} -1} \right ) = 3.27\times\mu_{R}
This derivation confirms that the published coefficients are based on the assumption that the monitored variable is Gaussian. Of course, it doesn’t prove it but it is highly unlikely that any other distribution would produce the exact same coefficients.
Interpretation
We need to consider the two charts separately.
The X chart
The X chart is simply a plot of the raw time series and, as long as the model X_{i} = C + W_{i} holds, 99.7% of the points will be within ±3σ of C. This is now commonly described as saying that the “p-value” of checking against these limits is 0.3%.
Generally, the p-value of a sample statistic is the probability that it will be outside its limits when all the data are generated from the reference model. P-values are often used today because they are more general and less arbitrary than levels of significance, and easy to calculate. A 95% level of significance means p=.05 and 99%, p=.01. Running multiple tests against the same data until you find one that gives you a “significant” difference is called p-hacking.
The mR chart
The p-value of the mR chart, however, is higher, meaning that it is more prone to false alarms. In terms of \sigma, the mR chart’s upper control limit is
3.27\times\mu_{R} = 3.69\sigma
and the standard deviation of the differences W_{i} - W_{i-1} is
\sigma_{D} = \sqrt{2}\times\sigma
If we plug these numbers into the formula for the cumulative distribution function of the half-gaussian, we get:
p = 1- erf(\frac{3.69}{2}) = 1\%
As can be easily verified with simulations, this yields an average of 1 false alarm for every 100 points, which is three times more than the X chart. If the process is unstable, there are so many genuine alarms for the engineering team to investigate that false alarms won’t be a problem.
If, on the other hand, it is so stable that it never goes out of control, the chart will still generate alarms and they will all be false. After two or three cases of assembling a task force to chase non-existent assignable causes, management will lose confidence in the chart.
Don Wheeler’s reasons for plotting mR charts
XmR chart expert Don Wheeler offers the following, not-fully compelling reasons to plot mR charts:
- “The Moving Range Chart will, on occasion, provide new information in addition to reinforcing the message of the X Chart.”
- “Thus, the mR Chart is the secret handshake of those who know the correct way of computing limits for an X Chart. Omit it and your readers cannot be sure that you are a member of the club.”
- “The mR Chart allows you and your audience to check for the problem of chunky data. This is a problem that occurs when the data have been rounded to the point that the variation is lost in the round-off.”
New information?
The mR chart is indeed a summary of the X chart and, as such, may provide new information. The questions are whether it is worth the trouble to maintain it and whether there are no other tools from time series analysis to get the same information more easily.
Club membership
The point of visualizing and analyzing quality characteristics is to troubleshoot a process, not to secure the approval of others or prove membership in any club. The inventors of these techniques didn’t have professional societies looking over their shoulders and checking their work for conformity to standards. The same problems should be addressed in the same spirit today.
Chunky data
“Chunky data” is a real problem. I remember a case where operators had manually measured the thickness of a plate at its four corners, with calipers that gave four significant digits, which they had rounded to two. Unfortunately, the information we were looking for was in the digits they had rounded off. We didn’t, however, need an mR chart to find out. It was visible in the paper spreadsheet. The risk of this happening is almost entirely eliminated in automatic data acquisition from sensors, instruments, and IIoT devices.
#XmR, #SPC, #ProcessBehaviorChart
March 2, 2019 @ 9:21 am
Michel,
Sweet derivation, not sure I could do those anymore. However, long ago I learned those fudge factors were based on the normal distribution and I am sure I could find it in some book of mine. However the person who said “…that the X-mR chart is a wonderful and currently useful process behavior chart, universally applicable, a data analysis panacea, and requiring no assumption on the structure of the monitored variables….” is not living in any world I have seen that might create data usable on a control chart.
A few years ago, like maybe 20…Donald Wheeler started hard selling the XmR and as Wheeler is a really bright guy, he could use it properly for for variety of data. That however is not true for eveyone. The interpretation of any control chart IS NOT INDEPENDENT of the raw data used. However in my practical experience the underlying assumption of normality is infrequently a limitation to process improvement.
This is due to two factors. Both the quality of the data and the quality of the process analyzed are so far from “good” that you do not need a very sharp instrument to make progress. However if you continue to work with that data and work with that process, it is important to understand the limitations of the tools you are using. You can carve a turkey with a 10″ kitchen knife or a surgeon’s scalpel ….. likewise you can take out an appendix with a either tool.
If you are going to use these tools, it usually works best if you understand them. I find that thought to be not only revolutionary but counter cultural to many trying to solve problems today…..
Nice posting
My 2 cents worth
November 7, 2021 @ 6:02 am
The three sigma limits work for the vast majority of distributions, no matter how skewed or heavily-tailed (see Understanding Statistical Process Control, Wheeler & Chambers, 1992).
November 7, 2021 @ 7:25 am
See my response from March 14,2019 to Scott Hindle in this thread. The universe of possible distributions, even for measured variables on products, is broader than anything Wheeler discussed.
March 2, 2019 @ 9:58 pm
How about averaging 5 or more data points and using the central limit theorem to make the average from a normal distribution?
March 5, 2019 @ 5:05 pm
This is just about working out the math behind a tool other people recommend. It’s about understanding it, not promoting or discouraging its use.
March 15, 2019 @ 8:37 am
I read this comment and I said, “Who is this guy and where has Michel Baudin gone??” I have known Michel for about 10 years mostly through blog postings and later when he proposed to exchange books we had respectively written. To me he was a very practical, hands on type of guy, so all this discussion of the math theory as it applied to a process improvement tool — totally threw me off. I could not believe what I was reading and I went on a journey to find my friend Michel. Lo and behold I found him in his bio, which obviously I had not read carefully enough, — it says, “trained in …. applied math”.
So now that I have found my friend I will bow out of this discussion, because although all this theory is interesting, when it comes to process improvements, it is largely, not completely, but largely irrelevant.
March 16, 2019 @ 7:16 am
You caught me. I have been a closeted mathematician for more than 35 years. After I pivoted to manufacturing in the early 1980s, I noticed quickly that being open about this background was not helping me be effective. Judy Dayhoff was a colleague of mine at the time. Yet I kept using it without saying so, believing that nothing is as practical as a good theory.
Many years later, one comment my editor at Productivity Press made about Working With Machines was that it started with building block and combined them logically into systems. “It’s like math,” he said. Pascal Dennis also noticed that, in Lean Logistics, the discussion of supplier-customer relationships is based on the theory of the Prisoner’s Dilemma from game theory. I didn’t say so in the book to avoid spooking my readers.
Some years later, on a project, I noticed an error in a formula used in a client spreadsheet to calculate safety stocks. It was a basic typo — one term that should have been squared was linear and vice versa — but it made the formula produce consequential nonsense. I was not familiar with that formula, and couldn’t find a derivation of it anywhere. So I worked it out and posted it in this blog. To my surprise, it’s been the second most popular post for years.
Times have changed, and so has technology. I have come out of the closet. I hope it doesn’t cost me your friendship.
March 3, 2019 @ 12:20 pm
Oh, yes, data are assumed to be normally distributed. Not the *underlying* data, but the means of those data (that’s why it’s called “Xbar” or “Xm”. See https://en.wikipedia.org/wiki/Central_limit_theorem.
I am not sure it’s true in the vast majority of cases, but I would tend to believe it’s true in most cases.
Or did I miss something? I am certainly no authority on this topic.
March 5, 2019 @ 2:59 pm
Great read Michel. I am currently doing similar calculations in my Customer Analytics course. I also want to use these equations as they may help me with a school project I am working on involving an inefficient cleaning process. I will be back for more, Thanks !
March 14, 2019 @ 4:40 am
In this free-to-access paper , Dr. Wheeler delves into the robustness of the d2 values that leads to the scaling factor of 2.66 (where 3/1.128=2.66) stated towards the start of this paper.
Hence, while the normal distribution provides the theoretical value of 1.128 for d2, Wheeler discusses what departures from normality mean in practice, not theory, where we have a limited no. of data and not an infinite amount.
I find XmR charts tremendously useful. The trick is in knowing how to use them to good effect. The “way of thinking” is the hard part I find. For example, how frequent should data be collected to achieve a meaningful, insightful XmR chart? The importance of this question is, I think, too little appreciated. Get the answer wrong and the XmR chart can be more problematic than helpful.
March 14, 2019 @ 4:17 pm
[latexpage]
If you don’t mind, I prefer to call the distribution “gaussian” rather than “normal” because of the implication in everyday speech that every other distribution is, in some way “abnormal.”
What I show in my post is that you can derive the control limits of the XmR chart straight from the properties of the gaussian distribution without introducing the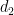 or
or 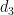 .
.
In his paper, Wheeler considers a limited range of distributions. They are all unimodal and just have nonzero skewness and kurtosis. The universe of possible product characteristics, however, is not this restrictive. Following are a few examples you might encounter:
April 2, 2019 @ 3:04 am
Hi Michel, I would hope nobody thinks an XmR chart is for “everything”. Like all “tools”, use it to bring value / clarity / insight… if not, the use may be unnecessary.
No doubt different people will prefer certain tools over others. I have just found, as said, that an XmR chart is tremendously helpful.
If we have output from two machines with two modes, but both have the same nominal value (target), see how to correct this and bring them back in line with each other. A time series or histogram may be sufficient to identify the problem and help define a good way forward / action plan.
I’d argue that key to XmR charts is “rational sampling”, not worrying about normality.
Thanks!
March 16, 2019 @ 8:35 am
Au contraire Michel, it is refreshing to find a renaissance man amongst my many lean geek friends. For Dr. Deming, there was no “profound knowledge” without an understanding of the underlying theory. What continues to amaze me is that practitioners, often very soft on the needed skills, but who are poised, polished speakers and have a fine vocabulary of lean terms can often sway the many neophytes they deal with. However, when the rubber meets the road, and they must actually perform, they find they come up short. They then need to “get back to the books” OR find a convenient excuse for the non performance. Which reminds me of one of my favorite quotes, by John Kenneth Galbraith, who said,
“In the choice between changing one’s mind and proving there’s no
reason to do so, most people get busy on the proof”.
And for those folks who are weak on the theory, I find they become exceedingly creative when it comes to “getting busy on the proof”.
I agree fully with Dr. Deming that you must understand the underlying theory of your trade, be it supply chain management, lean applications or skill sets like engineering, sales, supervision and management. If you do not understand the underlying theory you will be limited to the writings documenting what others have accomplished – under the limited environment in which they accomplished that. Almost surely your circumstances will differ by some degree. Well, you need to understand the underlying theory, that is, if and only if, you want to be good at your trade. Success is not mandatory.
Losing a friend, hardly, I just have a renewed appreciation for an old one. Be well
Michel, sorry this has little to do with the derivation of d2, but I could not resist… and again, be well
March 28, 2019 @ 6:42 am
Comment on LinkedIn:
March 28, 2019 @ 6:43 am
The vocabulary of the field has changed so much since those days that I have no idea what Shewhart meant by this. I am sure he meant something specific with “statistical universe” but I have no idea what. On the other hand, the math shows exactly how limits are calculated, whatever interpretation anyone wants to put on it.
March 28, 2019 @ 6:44 am
Comment on LinkedIn:
March 28, 2019 @ 6:47 am
The XmR charts plots individual values, not averages. The Xbar chart plots sample averages. The primary reason is to dampen fluctuations so that shifts in the mean stand out better.
The Central Limit Theorem (CLT), as you said, does make sample averages converge to a Gaussian, provided the individual values are independent and have a mean and a standard deviation.
The Statistical Quality establishment, however, denies that it has any relevance. I don’t know why.
A serious problem with relying on sample statistics is that you need samples. With one-piece flow, you don’t want to wait until you have 5 pieces. You use go/no-go gauges on every part to react immediately and mistake-proof your processes.
It only works if your quality is high enough. If your first-pass yield is <97%, it won’t work, and neither will one-piece flow.
In this case, you should focus on yield enhancement, which requires more advanced techniques than control charts.
March 28, 2019 @ 6:48 am
Comment on LinkedIn:
March 28, 2019 @ 6:45 am
In Shewhart’s Statistical Method From The Point Of View Of Quality Control (1939), I don’t see anything but an effort to apply the state of the art in probability and statistics as it was in his day.
Admirable though his work is, parsing his words from today’s vantage point is a scholastic exercise of limited value. Our time is better spent researching and advancing the current state of the art.
The bottom line is that SPC control charts for measurements have control limits based on the assumption that, while under statistical control, the measurements are the sum of a constant and fluctuations that form a Gaussian white noise.
However you wish to interpret what it means, that’s the math, and anyone can check it without quoting any authority.
March 28, 2019 @ 6:42 am
Comment on LinkedIn:
March 28, 2019 @ 6:43 am
The vocabulary of the field has changed so much since those days that I have no idea what Shewhart meant by this. I am sure he meant something specific with “statistical universe” but I have no idea what. On the other hand, the math shows exactly how limits are calculated, whatever interpretation anyone wants to put on it.
April 2, 2019 @ 3:24 am
Shewhart meant that SPC starts doubtful that a process will be “in control” (i.e. stable or predictable process). Without evidence of a reasonable degree of control (i.e. stable process) there is simply no probability model to talk about, neither gaussian nor other.
As an example, hypothesis tests, on the other hand, assume a stable process (e.g. iid data) and proceed without bothering to check this assumption/requirement… Yet, an unstable process undermines the interpretation of the hypothesis test.
While times have changed, and we should change with the times, the above holds true long after Shewhart’s pioneering work. When something new is better, embrace it. But if not, why change? Here we have a judgement call, people will see things in different ways…
March 28, 2019 @ 6:44 am
Comment on LinkedIn:
March 28, 2019 @ 6:45 am
In Shewhart’s Statistical Method From The Point Of View Of Quality Control (1939), I don’t see anything but an effort to apply the state of the art in probability and statistics as it was in his day.
Admirable though his work is, parsing his words from today’s vantage point is a scholastic exercise of limited value. Our time is better spent researching and advancing the current state of the art.
The bottom line is that SPC control charts for measurements have control limits based on the assumption that, while under statistical control, the measurements are the sum of a constant and fluctuations that form a Gaussian white noise.
However you wish to interpret what it means, that’s the math, and anyone can check it without quoting any authority.
March 28, 2019 @ 6:46 am
Comment on LinkedIn:
March 28, 2019 @ 6:46 am
Comment on LinkedIn:
March 28, 2019 @ 6:47 am
The XmR charts plots individual values, not averages. The Xbar chart plots sample averages. The primary reason is to dampen fluctuations so that shifts in the mean stand out better.
The Central Limit Theorem (CLT), as you said, does make sample averages converge to a Gaussian, provided the individual values are independent and have a mean and a standard deviation.
The Statistical Quality establishment, however, denies that it has any relevance. I don’t know why.
A serious problem with relying on sample statistics is that you need samples. With one-piece flow, you don’t want to wait until you have 5 pieces. You use go/no-go gauges on every part to react immediately and mistake-proof your processes.
It only works if your quality is high enough. If your first-pass yield is <97%, it won’t work, and neither will one-piece flow.
In this case, you should focus on yield enhancement, which requires more advanced techniques than control charts.
March 28, 2019 @ 6:48 am
Comment on LinkedIn:
April 2, 2019 @ 3:35 am
You claim “the measurements are the sum of a constant and fluctuations that form a Gaussian white noise. ” This is incorrect. Dr Wheeler proved Dr Shewhart’s assertion by showing that control charts work for 1143 different non Gaussian distributions, in his book “Normality and the Process Behavior Chart”.
May 29, 2019 @ 10:35 pm
It is what the math is based on. It doesn’t mean you can’t use it in a broader context. No real gas is ideal, yet chemists routinely apply the ideal gas law.
The point of working out the math behind a formula is not to restrict its use but to understand how far you are straying from its underlying assumptions.
March 8, 2022 @ 6:50 pm
Chebyshev’s theorem states that for any distribution, at least (1-1/k^2)% of the distribution will be between mu +/- k(sigma). For 3 sigma limits then, at least 89.9% of the distribution is expected to be contained within the control limits. However, this means that the false alarm rate for highly skewed distributions can be as much as 11.1%. We can cherry-pick well-behaved distributions to show a low false alarm rate, but why do so? There are tools available such as the AD test to check for non-normality. There are other charts with subgroup n =1 such as the EWMA that have protection against non-normality and are more sensitive to mean shifts. These can be created easily these days.
April 18, 2022 @ 11:44 am
It doesn’t apply to “any distribution” but only to those that have It is required to have an expected value and a standard deviation. It is not a trivial restriction, as it is quite easy to construct a random variable that has no expected value, such as the ratio of two Gaussian, centered measurement errors. It follows a Cauchy distribution, which has no expected value.
May 6, 2020 @ 3:46 am
Read Economic Control of Quality of Manufactured Product (Shewhart, 1931) and Statistical Method from the Viewpoint of Quality Control (Shewhart, reprint 1939). Dr. Donald J. Wheeler has published many books on the subject that clearly explains and address many misconceptions (e.g., normality, central limit theorem) for example (many more) Understanding Statistical Process Control, Advanced Topics in Statistical Process Control, Guide to Data Analysis.
May 6, 2020 @ 6:11 am
What exactly makes you think I am unaware of the writings of Shewhart or Wheeler?
April 19, 2021 @ 8:01 pm
Hi Michel,
I came across your article while seeking to understand control charts better as I am not one happy with plucked constants from thin air. I seemed to have missed a connection here in your derivation when you are calculating the mean. Could you possibly break that out a bit further on where you pull the mean of the range for the half gaussian?
Thanks,
Garrett
April 19, 2021 @ 8:39 pm
If you want more details on the Half-Gaussian, please check out the Wikipedia article about, to which I linked in the post.
April 20, 2021 @ 6:34 pm
Ah this was a reading comprehension error. I read the linked wikipedia but for some reason did not catch that. In any case thanks for this article much appreciated and grants some nice understanding.
November 7, 2021 @ 12:50 pm
Michel
I am not sure who your “sources” are that are telling you “the XmR chart is a wonderful and currently useful process behavior chart, universally applicable, a data analysis panacea, requiring no assumption on the structure of the monitored variables” but I would not spend too much time with them on the topic of SPC.
The first part “…the XmR chart is a wonderful and currently useful process behavior chart,” is fair enough. The remainder sounds like the rantings of a salesman trying desperately to meet his monthly quota.
An SPC chart is a model that is trying to explain the output of some variable(s). As a model, none are “…universally applicable”, none are “…..a data analysis panacea” , and none are free from the “….. assumption on the structure of the monitored variable.”
I have some concern that your sources characterize the XmR chart as being, “…currently useful”. They are somehow implying that they are new or, at an earlier time were not useful. Neither is factual. I first ran across XmR charts while studying a book, “Statistical Quality Control Handbook” published by AT&T in 1956. It documents much of the work done by Walter Shewhart (and others) starting in 1920 at Bell Labs. We oldtimers know this book by the name of “The Western Electric Handbook” and they have an excellent treatment of XmR charts.
Recently XmR charts have gotten a shot in the arm by Donald Wheeler and I think he may have even written a book centered on them. Someone even told me that Wheeler invented the XmR chart. Somehow I doubt that, If he did he was less than 12 years old at the time. When I took his SPC class (~1985) he taught XmR charts but made no big deal about them. About 5 years later I hired him to teach SPC to our engineers and he had more material on XmR charts.
The bottom line is they have a use and can be helpful. But like all tools and techniques, they have a “bounded applicability” and are useful within a range. But “universally applicable”, no way…. “a panacea for data analysis”, no way and “requiring no assumption on the structure of the monitored variables”, again, no way.
My nickels worth and be well
Lonnie
November 15, 2021 @ 4:53 am
You can see Wheeler’s take on the origin of the XmR chart at https://www.spcpress.com/pdf/DJW317.Jul.17.History%20of%20XmR%20Chart.pdf.
November 15, 2021 @ 9:36 am
Yeah, this is typical Wheeler as he makes the case for the broad applicability of the XmR chart. However, he falls short of saying it is “universally applicable” and states several limitations on it. For example under “Rational Sampling” he states:
“In order for the XmR chart to work as intended there are two things that need to happen. The first of these is that successive values need to be logically comparable. The second is that the moving ranges need to capture the routine variation of the underlying process. A time series that mixes apples and oranges together will not satisfy the two criteria above. You have to organize your data so that you are dealing with all apples or all oranges.”
He spends some time on rational subgrouping and quite frankly, that is the major problem I see in industry which is that too many want to just manipulate the numbers without understanding the context of the data and the utility of the techniques used. For example, a foot is 12 inches long and my foot has five toes, therefore the average toe length is 2.4 inches. There is a difference between manipulating the numbers and analyzing the data. He also sites “noise filled” data as needed treatment before they can be analyzed on a process behavior chart.
While I do not agree that Wheeler is saying they are “universally applicable” I appreciate your point as I have seen similar comments about XmR charts posted in blogs etc. XmR charts are simply a tool with a “bounded applicability” and are useful in that area.
My recommendation is still to ” … not spend too much time with them on the topic of SPC.”
Be well
November 15, 2021 @ 10:53 am
One thing he never discusses is that moving ranges are autocorrelated by construction, simply because two consecutive differences have a common term.
November 15, 2021 @ 11:08 am
I thought he discussed that, but maybe I am recalling from his classes many years ago but that principle gets lost on many people and they go crazy when they see one that data point on the X chart, may cause two out-of-control points on the mR chart. He is making his point and possibly he stresses the strengths and glosses over other issues such as the rules for reading the charts. I try to keep in mind that these process monitoring charts are our attempts as models and (I believe) it was Stuart Hunter, speaking of the DOE models, who said “All models are wrong, some are useful.” With that I concur .. universally. Be well
January 19, 2022 @ 9:43 pm
Michel Nice article on process behavior charts. We have a small team working to develop an easy to use tool in Excel and we have named it PBCharts. Please give it a try to see if it makes it easier. Comments appreciated!
Process Capability Indices – Michel Baudin's Blog
November 13, 2023 @ 9:09 pm
[…] coefficients that technicians, or SPC software, are supposed to use in setting limits. If you work out the math, however, it becomes clear that these coefficients are based on the Gaussian […]
Process Control and Gaussians
March 5, 2024 @ 2:22 pm
[…] The Math Behind The Process Behavior Chart (2019) […]