Nov 17 2011
Jidoka versus automation
Toyota’s jidoka isn’t just about stopping production when something goes wrong. It is an automation strategy that works because it is incremental and centered on human-machine interactions. It is essential to the strength of manufacturing in high-wage economies and should command more attention than it has so far among Lean implementers.
The most striking characteristic of automation in manufacturing is that, while making progress, it has consistently fallen short of expectations. In Player Piano, Kurt Vonnegut articulated the 1950s vision of automated factories: integrated machines produce everything while their former operators are unemployed and the managers spend their time playing silly team-building games at offsite meetings. 60 years on, the most consistently implemented part of Vonnegut’s vision is the silly team-building games…
Nippon Steel’s Yawata Steel Works in Kitakyushu, Japan, produce as much today with 3,000 employees as they did with 40,000 in 1964, and this transition was accomplished without generating massive unemployment. There are other such limited areas of automation success, like the welding and painting of car bodies. When manufacturing jobs are lost today, it is almost never to automation and almost always to cheaper human competition elsewhere. In the words of an experienced operator in a plant making household goods in the US, “When I joined 25 years ago, I expected these jobs to be automated soon, but we’re still doing them the same way.”
What is holding up automation today is not technology but the lack of consideration for people. There are entire books on automation without a paragraph on what their roles should be. Of course, a fully automatic, “lights-out” factory has nobody working inside, so why bother? There are at least two reasons. First, even an automatic plant needs people, to program its processes, tell it what work to do, maintain it, monitor its operations and respond to emergencies. Second, successful automation is incremental and cannot be developed without the help of the people working in the plants throughout the migration.
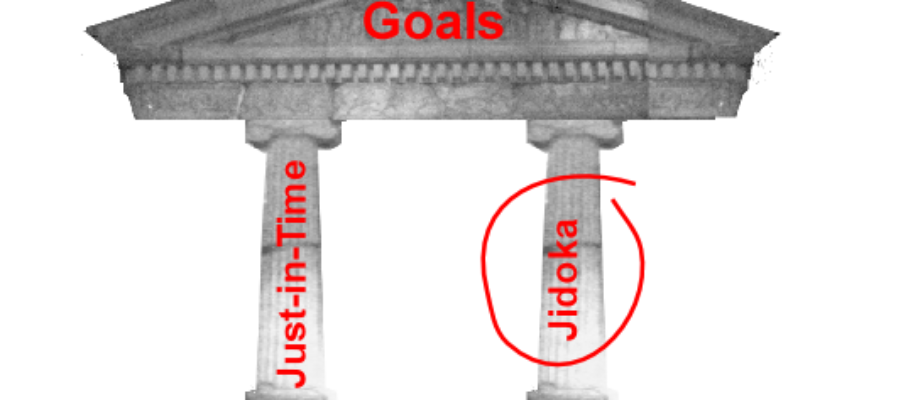
Enter autonomation, or jidoka, which is sometimes also called “automation with a human touch” but really should be called human-centered automation. Instead of systems of machines and controls, it is about human-machine interactions. In the classical House of Lean model, the two pillars holding up the roof at Just-In-Time and Autonomation, or Jidoka. Figure 1 is lifted from the introduction to Working with Machines, and shows what happens when the jidoka pillar is ignored.
 Figure 1. Just-in-Time and Jidoka
Figure 1. Just-in-Time and Jidoka
More and more, the Lean literature in English uses the japanese word jidoka rather than autonomation, but with its scope reduced to the idea of stopping production whenever anything goes wrong, and the concept is tucked away under the umbrella of Quality Management.
Toyota’s jidoka is a tricky term, because it is an untranslatable pun. Originally, the Japanese word for automation is jidoka (自動化) , literally meaning “transformation into something that moves by itself.” What Toyota did is add the human radical 人 to the character 動 for “move,” turning it into the character 働 for “work,” which is still pronounced “do” but changes the meaning to “transformation into something that works by itself.” It”s automation with the human radical added, but it is still automation, with all the technical issues the term implies.
The discussion of automation in the first draft of Working with Machines started with the following historical background, which was edited out like the chapter on locomotives and typewriters, on the ground that it contained no actionable recommendations. In this blog, I can let you be the judge of its value.
From tea-serving wind-up dolls to autonomation
The word automation was first used by Ford manufacturing Vice President Delmar Harder in 1947 for devices transferring materials between operations. He set as targets a payback period of at most one year in labor savings, which meant in practice that each device should not cost more than 15% above an operator’s average yearly wages and eliminate at least one operator. While this kind of economic analysis is still used, from the perspective of Toyota’s system, Ford’s focus on materials handling was putting the integration cart before the unit operation horse. Toyota’s approach focuses on individual operations first, and only then addresses movements of parts between them. In 1952, John Diebold broadened the meaning of automation to what has become the common usage, and painted a picture of the near future that was consistent with Kurt Vonnegut’s.
At that time, automatic feedback control was perceived to be the key enabling technology for automation, to be applied to ever larger and more complex systems. It was not a new concept, having been applied since 1788 in the centrifugal governor regulating pressure in a steam engine (See Figure 2)
Figure 2. James Watt’s 1788 centrifugal governor
Applying electronics to feedback control in World War II had made it possible, for example, to move a tank’s gun turret to a target angle just by turning a knob. Postwar progress in the theory and application of feedback control both caused many contemporary thinkers, like Norbert Wiener, to see in the concept a philosophical depth that is truly not there, and to underestimate what else would need to be done in order to achieve automation. Of course, if you cannot tell a machine to take a simple step and expect it to be executed accurately and precisely, then not much else matters. Once you can, however, you are still faced with the problem of sequencing these steps to get a manufacturing job done.
While automatic feedback control was historically central to the development of automatic systems, it is not at center stage in manufacturing automation today. With sufficiently stable processes, open-loop systems work fine, or feedback control is buried deep inside such off-the-shelf components as mass flow controllers, thermostats, or humidity controllers. Manufacturing engineers are occasionally aware of it in the form of variable-speed drives or adaptive control for machine tools, but other issues dominate.
Fixed-sequence and even logic programming also have a history that is as long as that of feedback control and are by no means easier to achieve. Figure 2 shows two examples of 18th century automata moved by gears, levers and cams through sequences that are elaborate but fixed.
Figure 2. 18th century automata from France and Japan
These concepts found their way into practical applications in manufacturing as soon as 1784, with Oliver Evans’s continuous flour mill that integrated five water-powered machines through bucket elevators, conveyors and chutes (See Figure 3). The same kind of thinking later led to James Bonsack’s cigarette making machine in 1881, and to the kind of automatic systems that have dominated high-volume processing and bottling or cartonning plants for 100 years, and to the transfer lines that have been used in automotive machining since World War II.
 Figure 3. Oliver Evans’ continuous flour mill (1784)
Figure 3. Oliver Evans’ continuous flour mill (1784)
Fixed-sequence automation works, but only in dedicated lines for products with takt times under 1 second, where the investment is justifiable and flexibility unnecessary. Rube Goldberg machines parody this type of automation.
 Figure 3. Winner of the 2008 Penn State Rube Goldberg machine contest
Figure 3. Winner of the 2008 Penn State Rube Goldberg machine contest
Automation with flexibility is of course a different goal, and one that has been pursued almost as long, through programmable machines. The earliest example used in production is the Jacquard loom from 1801, shown in Figure 4. It is also considered a precursor to the computer, but it was not possible to make a wide variety of machines programmable until the actual computer was not only invented but made sufficiently small, cheap and easy to use, which didn’t occur until decades after Vonnegut and Diebold were writing.
 Figure 4. Jacquard loom from museum in Manchester, UK
Figure 4. Jacquard loom from museum in Manchester, UK
By the mid 1980’s, the needed technology existed, but the vision of automation remained unfulfilled. In fact, more technology was available than the human beings on the shop floor, in engineering, and in management knew what to do with. As discussed in the post on Opinels and Swiss knives, the computer as a game changer. In manufacturing, this was not widely recognized when it became true, and it still is not today.
Writing in 1952, John Diebold saw nothing wrong with the way manufacturing was done in the best US plants, nor did he have any reason to, as the entire world was looking at the US as a model for management in general and manufacturing in particular. In the 1980’s, however, when GM invested $40B in factory automation, it was automating processes that were no longer competitive and, by automating them, making them more difficult to improve.
Whether the automation pioneers’ vision will ever come true is in question. So far, every time one obstacle has been overcome, another one has taken its place. Once feedback control issues were resolved came the challenge of machine programming. Next is the need to have a manufacturing concept that is worth automating, as opposed to an obsolete approach to flow and unit processes. And finally, the human interface issues discussed must be addressed.
21st century manufacturers do not make automation their overall strategy. Instead, automation is a tool. In a particular cell, for example, one operator is used only 20% of the time, and a targeted automation retrofit to one of the machines in the cell may be the key to eliminating this 20% and pulling the operator out of the cell.



Nov 18 2011
At 25, Toyota plant still lean, flexible, world-famous | Op-Ed | Kentucky.com
Via Scoop.it – lean manufacturing

An important milestone in automotive manufacturing is taking place with Toyota’s celebrated Georgetown plant marking its 25th anniversary on Monday.
Via www.kentucky.com
Share this:
Like this:
By Michel Baudin • Press clippings • 0 • Tags: Lean assembly, Lean manufacturing, Manufactuting, Toyota