Dec 27 2011
Is SPC obsolete?
In the broadest sense, Statistical Process Control (SPC) is the application of statistical tools to characteristics of materials in order to achieve and maintain process capability. In this broad sense, you couldn’t say that it is obsolete, but common usage is more restrictive.
The semiconductor process engineers who apply statistical design of experiments (DOE) to the same goals don’t describe what they do as SPC. When manufacturing professionals talk about SPC, they usually mean Control Charts, Histograms, Scatter Plots, and other techniques dating back from the 1920s to World War II, and this body of knowledge in the 21st century is definitely obsolete.
Tools like Control Charts or Binomial Probability Paper have impressive theoretical foundations and are designed to work around the information technology of the 1920s. Data was recorded on paper spreadsheets, you looked up statistical parameters in books of tables, and computed with slide rules, adding machines or, in some parts of Asia, abacuses (See Figure 1).
In Control Charts, for example, using ranges instead of standard deviations was a way to simplify calculations. These clever tricks addressed issues we no longer have.
Figure 1. Information technology in the 1920s
Another consideration is the manufacturing technology for which process capability needs to be achieved. Shewhart developed control charts at Western Electric, AT&T’s manufacturing arm and the high technology of the 1920s.
The number of critical parameters and the tolerance requirements of their products have no common measure with those of their descendants in 21st century electronics.
For integrated circuits in particular, the key parameters cannot be measured until testing at the end of a process that takes weeks and hundreds of operations, and the root causes of problems are often more complex interactions between features built at multiple operations than can be understood with the tools of SPC.
In addition, the quantity of data generated is much larger than anything the SPC techniques were meant to handle. If you capture 140 parameters per chip, on 400 chips/wafer and 500 wafers/day, that is 28,000,000 measurements per day. SPC dealt with a trickle of data; in current electronics manufacturing, it comes out of a fire hose, and this is still nothing compared to the daily terabytes generated in e-commerce or internet search (See Figure 2).
 Figure 2. Data, from trickle to flood, 1920 to 2011
Figure 2. Data, from trickle to flood, 1920 to 2011
What about mature industries? SPC is a form of supervisory control. It is not about telling machines what to do and making sure they do it, but about checking that the output is as expected, detecting deviations or drifts, and triggering human intervention before these anomalies have a chance to damage products.
Since the 1920s, however, lower-level controls embedded in the machines have improved enough to make control charts redundant. The SPC literature recommends measurements over go/no-go checking, because measurements provide richer information, but the tables are turned once process capability is no longer the issue.
The quality problems in machining or fabrication today are generated by discrete events like tool breakage or human error, including picking wrong parts, mistyping machine settings or selecting the wrong process program. The challenge is to detect these incidents and react promptly, and, for this purpose, go/no-go checking with special-purpose gauges is faster and better than taking measurements.
In a nutshell, SPC is yesterday’s statistical technology to solve the problems of yesterday’s manufacturing. It doesn’t have the power to address the problems of today’s high technlogy, and it is unnecessary in mature industries. The reason it is not completely dead is that it has found its way into standards that customers impose on their suppliers, even when they don’t comply themselves. This is why you still see Control Charts posted on hallway walls in so many plants.
But SPC has left a legacy. In many ways, Six Sigma is SPC 2.0. It has the same goals, with more modern tools and a different implementation approach to address the challenge of bringing statistical thinking to the shop floor.
That TV journalists describe all changes as “significant” reveals how far the vocabulary of statistics has spread; that they use it without qualifiers shows that they don’t know what it means. They might argue that levels of significance would take too long to explain in a newscast, but, if that were the concern, they could save air time by just saying “change.” In fact, they are just using the word to add weight to make the change sound more, well, significant.
In factories, the promoters of SPC, over decades, have not succeeded in getting basic statistical concepts understood in factories. Even in plants that claimed to practice “standard SPC,” I have seen technicians arbitrarily picking parts here and there in a bin and describing it as “random sampling.”
When asking why Shewhart used averages rather than individual measurements on X-bar charts, I have yet to hear anyone answer that averages follow a Bell-shaped distribution even when individual measurements don’t. I have also seen software “solutions” that checked individual measurements against control limits set for averages…
I believe the Black Belt concept in Six Sigma was intended as a solution to this problem. The idea was to give solid statistical training to 1% of the work force and let them be a resource for the remaining 99%.
The Black Belts were not expected to be statisticians at the level of academic specialists, but process engineers with enough knowledge of modern statistics to be effective in achieving process capability where it is a challenge.





December 27, 2011 @ 12:56 pm
Nice historical view.
Modern SPC is really Statistical Monitoring and Adjustment, as Box and Hunter have pointed out, leaving realtime control to the automation folks, but setting up a hierarchy of monitoring to catch bad sensors or drifting tools for example. In the 1990’s sensor-based fault detection was added in the semiconductor industry, slowly, along with run-to-run adaptive control (adjustments based on models) and in this 21st century that evolved further. Earlier, in the “process” industries such as oil refineries and chemical plants, multivariate statistical process monitoring, sensor-based fault detection, and process tuning algoritms were developed. So if you like, you can say Old SPC >>> New SPM&A but it does not have a “ring” to it. Even in the 1920’s, SPC was really an open-loop human-intervention system of long-feedback not realtime control. So to that extent, nothing has changed in my opinion except the sensorization and automation improvements, and the massive amount of useful or misleading data that creates to be sorted out by experts or expert systems.
December 28, 2011 @ 5:14 am
Old SPC based on manual control charts produced by operators with pencil and paper by sampling may be dead specially in automatically controlled processes.
But we should not forget that we still have lots of manual processes and some automatic processes where process parameters can not be calculated theoretically (for instance solder processes).
When inspection and test data is collected automatically SPC charts based on 100% control could be made available to the operators in real time in order to detect trends which require immediate operator action and also avoid operator over-reaction (treating common cause variability as a special cause).
SPC concepts, as explained by E. Deming, are also important for Management in order to interpret data adequately specially nowadays when instant data is available in real time. I have seen many instances of management over-reaction and tampering leading to an increase of variability and process degradation.
It is true that a capable process (Cpk > 1.5) might not require any control, but unfortunately the state of the art in many processes is far from that.
December 28, 2011 @ 7:15 am
In Lean plants, you normally have team boards with charts of multiple metrics showing actual performance over time against target values.The metrics of quality usually include a first-pass yield and a list of problem reports traced back to the team. The use of these boards by team leaders and supervisors leaves traces in the form of manual annotations.
Even in manual processes, I don’t recall ever seeing a Shewhart-style control chart on any of these boards. The only place I recall seeing them in in hallways that visitors go through, beautifully printed, and free of manual annotations.
April 6, 2017 @ 1:31 pm
Have you read the work of Donald J. Wheeler, including his book “Understanding Variation?” His “process behavior charts” are SPC charts applied to the type of management data that you’d see on team boards. Even without a formal SPC chart, teams would be much better served by a manager realizing they shouldn’t overreact to every up and down in the data if it’s stable over time (the SPC chart can tell us if performance is stable and predictable). I don’t think this method is obsolete at all. Instead of asking for a dubious “root cause” for every below average data point, SPC thinking can help save time and allow us to focus on reacting to “signal” instead of “noise.” And, asking “how do we improve the system?” (reducing common cause variation) is far better than asking “why did we have a bad day yesterday?”
April 7, 2017 @ 6:35 am
Yes. as Nate Silver would put it, you need to tell the signal from the noise. As I wrote at the start of my post, I have no issue with using statistics to improve process capability. My concern is the overemphasis on 90-year old methods to do it. The whole quality profession needs to up its game and learn modern data science.
Japanese stock traders still use the candlestick charts invented by Munehisa Honma, a rice merchant who died in 1803. He also invented futures trading and used the charts to find patterns in rice prices that he used to make a fortune. Even though it was a wonderful tool, the traders who still rely on it today might think of including a few more recent ones.
And I still own a slide rule, as a souvenir.
December 30, 2011 @ 8:06 am
“In the broadest sense, Statistical Process Control (SPC) is the application of statistical tools to characteristics of materials in order to achieve and maintain process capability.”
This is a great point, one I end of having to remind people of all the time. Shewhart’s charts are not the entirety of statistical Process control – only a subset. The notion that they are always applicable is unfounded – although they are very handy where they do fit.
“Tools like Control Charts or Binomial Probability Paper have impressive theoretical foundations and are designed to work around the information technology of the 1920s.”
There are still many shop floors where the cost structure supports the technology of the ‘20s. In many places I end up having to utilize paper charting because many of the SPC programs do not offer the correct chart for the application.
“Another consideration is the manufacturing technology for which process capability needs to be achieved.” “What about mature industries? SPC is a form of supervisory control. It is not about telling machines what to do and making sure they do it,”
This is true – but not entirely the death knell of SPC. What I have found in precision machining is that the variation that may have been seen in 1930 may very well have done well with Shewhart charts. But at higher precision, Xbar-R charts actually encourage overcontrol and ignore critical with-in part variation. X bar- charts create unreasonably tight control limits, because they use the wrong statistics. They end up frustrating operators, and cause implemeters to make up “special rules” for machining that are still not correct. To them, it may seem obsolete – but wrong and obsolete are two different things. A more modern – yet still simple approach, the X hi/lo-R chart resolves many of these issues. It makes charting not only monitoring for special causes, but provides feedback to the operator when to make adjustments and when to change tools. It can accurately compare the improvement of one type of tool to another. The things Xbar-R charts do in precision machining is plot measurement error from samples of statistically insignificant size. What kind of decisions can be made from that? X hi/lo-R is even better information than automatic tool wear adjustment algorithms. They will mask valuable data with their overcontrol.
Blind rubber stamping of X-bar R charts can lead to frustration and ultimately its demise on the shop floor. You need to do your upfront work. You need to have a proper understanding of what is common or special cause. A simple thing of not doing a CNX evaluation of the process variable to see if you are charting noise or a true variable that can affect output. You need to do your FMEA to know ahead of time possible reaction plans, so you are not standing there staring at the chart as your process wanders off. You need to pick the correct chart for the process. Also, charting with “no one paying attention to the charts” is a sure death of the implementation.
“I believe the Black Belt concept in Six Sigma was intended as a solution to this problem.”
If we rubber stamp black belt concepts the way we rubber stamp capability indices and X-bar R charts, there will be little improvement in the overall picture.
To add to those comments, it also helps when it is implemented correctly. The key is, you have to *think.* As much as people think SPC is plug and chug, or as much as they wish it was, it is not. You have have to actually think. If you are not willing to make that investment, be prepared to fail. But, remember, wasting a resource is much different than obsolete. Much different. Chances are, if you *think* it is obsolete, you really have done it wrong. Those are the messes I end up having to clean up.
December 30, 2011 @ 2:26 pm
As you say, “There are still many shop floors where the cost structure supports the technology of the ‘20s.”
While it is true that many shop floors still use the information technology of the 1920s, I am not sure it is a question of cost. I still own an Aristo 0968 slide rule with a magnifying cursor from my student days, but I would never use it to get work done. In operations, it may have been wise to ignore the information technology of the 1960s and 70s, when computers were still expensive, hard-to-use clunkers, but I don’t think it is today.
December 30, 2011 @ 5:50 pm
Comment from Joseph (Joe) E. Johnson in the Continuous Improvement, Six Sigma, & Lean Group on LinkedIn:
December 30, 2011 @ 5:52 pm
Comment from Steve Ruegg in the Continuous Improvement, Six Sigma, & Lean Group on LinkedIn:
December 30, 2011 @ 5:59 pm
Comment from Bob Mallett in the Continuous Improvement, Six Sigma, & Lean Group on LinkedIn:
December 30, 2011 @ 6:00 pm
Comment from Attila Fulop in the Continuous Improvement, Six Sigma, & Lean Group on LinkedIn:
January 2, 2012 @ 9:10 am
Comment in the Lean Six Sigma discussion group on LinkedIn:
January 2, 2012 @ 9:16 am
Comment in the Lean Six Sigma discussion group on LinkedIn:
January 2, 2012 @ 9:17 am
Comment in the Lean Six Sigma discussion group on LinkedIn:
January 2, 2012 @ 9:14 am
Comment in the Lean Six Sigma discussion group on LinkedIn:
February 8, 2013 @ 10:16 pm
Sanda, Super reply!
January 2, 2012 @ 1:00 pm
Comment in the Operational Excellence discussion group on LinkedIn:
January 2, 2012 @ 5:37 pm
I don’t think one can ever claim that a “scientific” tool like SPC is dead or obsolete. One can make a distinction however, between being able to “tell when the process has gone out of control” and ” error-proofing the process” so the former doesn’t even occur! Additionally, any repeatable and sustainable tool/system should be simple enough for the people at the Gemba (Shop-Floor) to understand, implement and then teach. Many “Lean” places do exactly that, where the Team Members on the floor use primitive monitoring & recording tools namely pencils and paper to do SPC charts and arrive at intelligible understandings.
All & all, SPC may not be as fashionable as it once was, it may have given way to Poka-Yoke and alike, but as a systematic and scientific approach, it is not disputable!
January 3, 2012 @ 12:59 am
Comment in the SME Society of Manufacturing Engineers discussion group on LinkedIn:
January 3, 2012 @ 1:00 am
Comment in the SME Society of Manufacturing Engineers discussion group on LinkedIn:
January 3, 2012 @ 1:01 am
Comment in the SME Society of Manufacturing Engineers discussion group on LinkedIn:
January 3, 2012 @ 1:02 am
Comment in the SME Society of Manufacturing Engineers discussion group on LinkedIn:
January 3, 2012 @ 1:04 am
Comment in the SME Society of Manufacturing Engineers discussion group on LinkedIn:
January 3, 2012 @ 1:05 am
Comment in the SME Society of Manufacturing Engineers discussion group on LinkedIn:
January 3, 2012 @ 1:07 am
Comment in the SME Society of Manufacturing Engineers discussion group on LinkedIn:
January 3, 2012 @ 7:13 am
Comment in the ASQ – The American Society for Quality discussion group on LinkedIn:
January 3, 2012 @ 7:17 am
Comment in the ASQ – The American Society for Quality discussion group on LinkedIn:
January 3, 2012 @ 7:19 am
Comment in the ASQ – The American Society for Quality discussion group on LinkedIn:
January 3, 2012 @ 7:22 am
Comment in the ASQ – The American Society for Quality discussion group on LinkedIn:
January 3, 2012 @ 7:24 am
Comment in the ASQ – The American Society for Quality discussion group on LinkedIn:
January 4, 2012 @ 9:55 am
Although I mean everything I wrote in the post that started this discussion, the title was intended to provoke responses, and it did. While most of you think SPC is not obsolete, none claims that it is embedded in daily shop floor practices and making a clear and obvious contribution to performance. You are saying that it has the potential to do so: it could, and it would, if only it were implemented correctly and supported by management.
I didn’t see the testimonial of a passionate practitioner who could inspire a 25-year old engineer to get involved. Such a testimonial might go as follows:
I would not expect this story to be true everywhere or even in a majority of plants. I would settle for one. This is the vision you get from the SPC literature. However, in 30 years in Manufacturing, I have never seen it realized anywhere.
These techniques have been around for almost 90 years. Deming died 19 years ago; Shewhart, 45 years ago. How much longer should we wait?
January 4, 2012 @ 10:04 am
Comment in the SME Society of Manufacturing Engineers discussion group on LinkedIn:
January 4, 2012 @ 10:12 am
Comment in the Continuous Improvement, Six Sigma, & Lean Group on LinkedIn:
January 4, 2012 @ 10:37 am
What I had said in my original post was, essentially, that statistical process control was still relevant but SPC was obsolete. The following experience I had a long time ago might throw light on what I mean by this distinction.
At the time, I was working on the specifications of a statistical process control software module for semiconductor wafer processing. In this process, you made hundreds of dies per wafer and processed the wafers in lots of 24. It struck me that it made sense to monitor separately the variability within wafers, between wafers in a lot, and between lots, as due to different causes.
It was not overly difficult to structure the data to produce plots with control limits that made statistical sense for all these different levels of variability. The quality managers in the plants, however, refused this idea, on the ground that it didn’t conform to the SPC standards as set by Shewhart in the Western Electric Statistical Quality Control Handbook.
I agree with your semantics, but I didn’t invent the restrictive small box you are talking about: I found myself standing outside of it.
January 5, 2012 @ 6:22 am
Comment in the ASQ – The American Society for Quality discussion group on LinkedIn:
January 6, 2012 @ 3:57 pm
Comment in the ASQ – The American Society for Quality discussion group on LinkedIn:
January 6, 2012 @ 3:58 pm
Comment in the ASQ – The American Society for Quality discussion group on LinkedIn:
January 6, 2012 @ 4:03 pm
Comment in the Lean Six Sigma discussion group on LinkedIn:
January 13, 2012 @ 6:32 pm
Comment in the SME Society of Manufacturing Engineers discussion group on LinkedIn:
January 13, 2012 @ 6:34 pm
Comment in the SME Society of Manufacturing Engineers discussion group on LinkedIn:
January 13, 2012 @ 7:05 pm
In the art of analyzing data, nothing has been frozen for the past 80 years except standard SPC, and, frankly, it is to the state of the art as a slide rule is to an iPad. My slide rule still works, and I could still use it if I had to. I wouldn’t be very good at it because I have not needed it for decades.
Computers have been invented since standard SPC was developed. Statisticians have developed numerous techniques that require computers and enable manufacturing engineers to solve process variability problems that are beyond the range of standard SPC. As I indicated earlier, these techniques are extensively used, for example, in semiconductor process development, but they are called “yield enhancement” rather than SPC.
January 13, 2012 @ 6:36 pm
Comment in the SME Society of Manufacturing Engineers discussion group on LinkedIn:
January 13, 2012 @ 6:39 pm
Comment in the SME Society of Manufacturing Engineers discussion group on LinkedIn:
January 13, 2012 @ 11:11 pm
Comment in the Lean & Six Sigma Community discussion group on LinkedIn:
January 13, 2012 @ 11:12 pm
Comment in the Lean & Six Sigma Community discussion group on LinkedIn:
January 13, 2012 @ 11:14 pm
Comment in the Lean & Six Sigma Community discussion group on LinkedIn:
January 15, 2012 @ 6:24 am
Comment on Michel Baudin’s LinkedIn page:
January 15, 2012 @ 11:43 am
Comment in the Continuous Improvement, Six Sigma, & Lean Group discussion group on LinkedIn:
January 15, 2012 @ 11:48 am
Comment in the Continuous Improvement, Six Sigma, & Lean Group discussion group on LinkedIn:
January 15, 2012 @ 11:49 am
Comment in the Continuous Improvement, Six Sigma, & Lean Group discussion group on LinkedIn:
January 15, 2012 @ 11:51 am
Comment in the Continuous Improvement, Six Sigma, & Lean Group discussion group on LinkedIn:
Author: High Quality at Economic Cost–Concepts, Approaches, Techniques in Design and Manufacture
January 15, 2012 @ 11:53 am
Comment in the Continuous Improvement, Six Sigma, & Lean Group discussion group on LinkedIn:
January 15, 2012 @ 11:55 am
Comment in the Continuous Improvement, Six Sigma, & Lean Group discussion group on LinkedIn:
MIT article comparing Lean, TQM, Six Sigma, “and related enterprise process improvement methods” | Michel Baudin's Blog
December 29, 2012 @ 3:17 pm
[…] approach to the enhancement of enterprise performance, what you find is a modernization of the SPC of the 1930s for the purpose of addressing the process capability issues of high-technology manufacturing. In […]
February 5, 2013 @ 10:12 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 5, 2013 @ 10:15 am
I do not understand your objection to my broad definition of SPC. The only difference with the one in Wikipedia is that, instead of calling it a method, I broaden the scope to the use of any statistical tool towards the same purpose. To me, it is a subset of SQC, which also includes, for example, tools to design final inspections on outgoing products that have nothing to do with process capability.
The reason I think it should be broadened is that I fail to see any value in restricting yourself to a fixed set of tools from 80 years ago. Neither manufacturing, nor statistics, nor information technology have been asleep in that time.
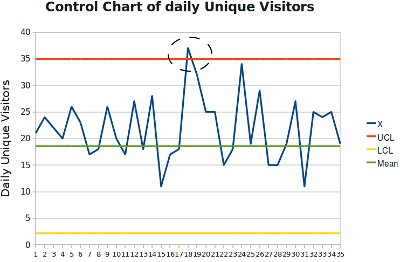
Range and Standard Deviations both measure spread. In the case of the XmR charts, since you only consider two data points, they are identical except for a constant factor of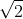 . For larger samples, the range R is easier to calculate than standard deviation S, as can be seen from the formulas for both:
. For larger samples, the range R is easier to calculate than standard deviation S, as can be seen from the formulas for both:
It made a difference manually. but doesn’t with software. Other than that, I don’t see any reason to use ranges rather than standard deviations.
February 5, 2013 @ 10:45 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 6, 2013 @ 9:16 am
You say: “No other technique can boast the same combination of ease of use and statistical sophistication as the control chart.”
“Ease of use” is not a term I would apply to control charts. Shop floor operators are much more comfortable with go/no-go gauges, stop ropes and Andons than with an Xbar-R chart. Even the best application attempts I have seen were riddled with mistakes and confusion, for example comparing sample averages with tolerances for individual values.
And, yes, it was sophisticated and clever statistics in 1930. The field has not been asleep since.
“SPC’s empirical approach has been the dominant investigative technique for 400 years and shows no signs of faltering.”
Are you equating SPC with the scientific method in general? Otherwise, I can’t figure out what you mean by “400 years.”
Dan Strongin and you repeatedly invoke Shewhart, Deming and Wheeler about the irrelevance of the normal distribution to Control Charts. What I see them doing is using the math of the normal distribution to compute all the parameters with which to set limits and issue alarms, and then vigorously assert that it makes no difference.
There is a branch of Statistics called non-parametric, distribution-free, or robust, in which you find confidence intervals about data without making any assumption on their distributions. But Control Charts are not that way.
If I were to argue the case, I would do it otherwise. Chemists routinely apply perfect gas formulas to gasses they know are not perfect. This is justified whenever the added accuracy of an exact formula would not change whatever decision you are making. You could argue that Control Charts are doing the same.
You could also say that measurements are not just any random variables and that the actual departures from normality that you observed are mild enough not to invalidate the method. They may depart from normality in being skewed, more concentrated around the mean, or less concentrated around the mean, but you don’t expect physical measurements on work pieces coming out of the same machine to have multiple modes or have a distribution without a mean or standard deviation.
You could add that training large numbers of people to use control charts in a variety of contexts is complex enough as it is, and that taking into account multiple distributions would have made it impossible…
Instead of making this kind of arguments, Shewhart, Deming and Wheeler just assert that the concerns are invalid. I read Wheeler’s criticism of the “Probability Approach to Control Charts” as trying to have it both ways. You can’t simultaneously use probability theory to calculate your parameters and dismiss it as irrelevant.
Yes, the Central Limit Theorem brings sample averages closer to normality than individual values, but that applies only to Xbar charts. Shewhart invokes Chebysheff’s inequality but it only gives you a 91% probability of having all data within three sigmas of the mean for just about any distribution that has a mean and a standard deviations. Extensions of this inequality for unimodal and for symmetric distributions give you a higher confidence, but not the 99.73% probability that you get with normality. And, in Statistical Method from the Viewpoint of Quality Control, Shewhart repeatedly quotes this “99.7%.” It also strikes me as trying to have it both ways.
August 27, 2018 @ 4:59 am
May I suggest that you read Dr Shewhart more closely. P68 for example. He gives ample background to his mention of 99.7. This is NOT the basis for control charts, nor is CLT, nor is Chebyshev.
“Statistical control [is] not mere application of statistics … Classical statistics start with the assumption that a statistical universe exists, whereas [SPC] starts with the assumption that a statistical universe does not exist.”
Dr Wheeler validates that control charts work for ANY distribution in his book “Normality and the Process Behavior Chart”
August 28, 2018 @ 3:14 pm
99.7% is the probability that a Gaussian with mean μ and standard deviation σ is within μ ± 3σ, end of story.
When Shewhart wrote “classical statistics,” it was in 1939, long before any American university even had a Statistics Department. The field, and the vocabulary to describe it, have changed massively since. I am sure he meant something specific with “statistical universe” but I have no idea what. Neither does Wikipedia, which has a page — accurate or not — on just about everything. But the page “statistical universe” does not exist.
Thanks for the book reference. I had read an article by Wheeler on this subject. I didn’t he had written a whole book on this. Based on the title, it looks like yet another plug for the vintage 1942 XmR chart as the solution to all problems and I have read enough on this topic. To expand your mind, how about reading E.T. Jaynes’ Probability, the Logic of Science from 2003.
February 5, 2013 @ 11:13 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 5, 2013 @ 11:17 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 5, 2013 @ 11:19 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 5, 2013 @ 11:23 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 6, 2013 @ 8:17 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 6, 2013 @ 8:21 am
I don’t have a one-size-fits-all answer, but here are a few partial one, including some previously given in the discussion on Lies and Statistics.
A rotary cement kiln is not something you would consider high technology, and it has parameters like temperature, pressure, flow times, humidity, and others that influence the outcome. Hirotsugu Akaike was a statistician I met in Japan in 1980 who worked on this problem and proposed a solution that involved a multidimensional autoregressive-moving-average (ARMA) model, with the use of what has since become known as the Akaike Information Criterion (AIC) to prevent overfitting. His approach was implemented in software and commercialized in Japan for embedding in kiln controllers. Admittedly, it works upstream from SPC, on the control parameters of the process rather than on its output, but it is statistics applied to process capability.
More generally, many machines now have computer controls. In the 1930s, none did. These controllers — whether they are CNCs, PLCs, SCADA systems, or custom-developed — make sure the machines follow the right sequence of steps, with the proper parameters, be they feeds and speeds, flow rates, temperatures, pressures, etc., so that what is done to each workpiece is much more tightly controlled than 80 years ago.
Often, these controllers can take measurements on the workpiece itself, using, for example, spindle probes in machining centers, eliminating the need for operators to do it. Based on these and other sensors, the controllers issue alarms and stop the machines as needed to prevent the production of defectives. This is part of Jidoka.
If that is not enough, you incorporate go/no-go checking with a gauge into the manual transfer between machines. SPC specialists prefer measured variables to go/no-go attributes on the grounds that a measurement is richer information. The difference here, however, is between a go/no-go check on every part as it comes off the machine, and measurements that you cannot afford to make on every part. If you have a policy of immediately stopping the machine when it makes a defective part, the go/no-go check on every part can provide better and more timely information.
Then you have Andon lights to communicate the status of the equipment and ensure a prompt response.
I didn’t mention mistake-proofing, because it is about preventing human error rather than detecting process capability problems. It is key to achieving high levels of quality, once you have achieved process capability. It is a 3rd-level technique.
First, you use statistical methods and process knowledge to achieve process capability. That’s Level 1. It gets you to 3% defective.
Then you change production to one-piece flow lines with go/no-go gauge checking as needed between operations. This provides rapid detection of discrete problems like tool breakage. That’s Level 2, and it gets you to 0.3% defective.
The main problem then becomes human error, and mistake-proofing then gets you to 15 ppm. That’s Level 3.
Level 4 is the combination of Change-Point Management and JKK (Jikotei Kanketsu).
February 8, 2013 @ 11:18 pm
After going through these discussions I am convinced that SPC is not Obselete! In my opinion SPC will not be dead. While working in Manufacturing set-up during initial part of my career, SPC concepts were relevant and used. As I moved to software industry, SPC concepts were of little use and analysis were subject to everyone interpretation! I also observed lot of resistance to use SPC concepts from development and management community (There are exceptions though!). Even I thought it was DEAD!
I suggest that there should be a serious change in the way SPC concepts are taught today (Who does? I don’t know!). I feel books and syllabus should give room for relevant case studies from different industries. Teaching methods should target people who use it not elite and learned. Objectives should be a) To teach most commonly used SPC tools in today’s context , 2) Where and when applicable and c) To help users to interpret probable outcome(s) and arrive at common conclusions.
As Sanda, stated earlier, the rule applied by users is that, “what you do not understand, you reject… ”
” If you don’t use it, you lose it”…. Matthew 25: 14-30
Question is, how do we continue to use well conceived concepts by our gurus? That too without common understanding among us? and Without a plan to carry the legacy forward?
Thanks to every contributor here for giving so much of learning experience 🙂
February 6, 2013 @ 8:20 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 6, 2013 @ 9:22 am
Question 1 – Are control limits both economic and probability limits?
Question 2 – Was individual chart used by Shewhart?
Question 3 – Is this true that Shewhart is not attributed to XmR charts?
Question 4 – Is there evidence that 3-sigma limits always provide the right balance for all processes, all conditions and all costs?
Question 5 – If anyone knows of any studies that support t=3 vs. any other value for i) various Type I and II errors, ii) various costs resulting from those errors, and iii) other multipliers than 3, please send me the references of the studies.
Question 6 – Is Deming wrong about control charts not being tests of hypotheses?
February 6, 2013 @ 9:07 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 6, 2013 @ 9:10 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 6, 2013 @ 9:30 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 6, 2013 @ 9:32 am
You wrote: “Before SPC understanding could mature, it took off in the direction of becoming a system, as opposed to becoming a problem-solving tool.”
I think what you mean is that it became a ritual. Such is the common fate of all approaches that become the focus of external audits. Regardless of whether it works or not, it has to look a standard way for the auditors to tick off the items in their checklist and certify you.
You wrote: “The definition that I go with for SPC is — SPC is not about statistics, process control or conformance to specifications. While it can be used in all of these ways, SPC is much more than any one of these narrow interpretations.”
If it’s not about statistics and process control, then why is it called “Statistical Process Control’? And it is process control in an unusual sense of the term. Outside of SPC, process control refers to programming automatic machines and making sure they follow instructions, by means, for example, of feedback control loops. In SPC, on the other hand, it is focused on the output of the process and the goal of achieving and maintaining process capability.
Narrow interpretations are good. Narrow interpretations support communication. With brosd interpretations, everything is everything, and we cannot have a conversation and know exactly what the other person is talking about.
I was surprised to find Shewhart’s own words equating quality with conformance to specification. Of course, in general, we don’t do this anymore but, when you are worrying about process capability, it is still what you have to do. If you get the process to routinely make parts with critical dimensions within tolerances, the job of SPC is done for now; the job of quality assurance is not.
Shewhart’s view of continuous improvement is cycling through specification, production and inspection, which I take to mean that, whenever you have achieved process capability, you tighten the tolerances and do it again. He may have been the first one to express this view. I don’t recall any notion of continuous improvement in the works of Taylor or even Gilbreth. To them, there was a “one best way,” and, once you had found it, by definition, you couldn’t improve on it. It was an optimization rather than a continuous improvement mindset.
This being said, I see no reason to call “SPC” everything that is intended to “improve processes and outcomes.” Techniques like Andon, successive inspection, mistake-proofing, cells, kanbans, etc., are used in continuous improvement but nobody would consider them part of SPC.
In business, it is common for acronyms to be disconnected from their original meaning. When NCR and KFC respectively expanded beyond cash registers and fried chicken, their names no longer meant “National Cash Register” and “Kentucky Fried Chicken.” But it doesn’t usually happen with ideas. “SPC” was introduced as a short way to say “Statistical Process Control,” and I see no value in using it to mean anything else.
February 6, 2013 @ 9:35 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 6, 2013 @ 9:38 am
I have to be very careful in my choice of words. I meant automatic feedback control, the kind you got 200 years ago in a steam pressure regulator with rotating balls and now with PID boxes.
The Taguchi definition you quote still strikes me a too narrow a view of quality. I go with Juran’s “agreement of reality with expectancy.” It is centered on customer experience and treats parameters you can measure as substitute characteristics.
In the paragraph about the job of SPC, the key phrase was “for now,” with the next paragraph elaborating on Shewhart’s cycle and its historical significance, as I see it.
I don’t understand your concern about the last two paragraphs. To me, if you use statistical tools, whatever they may be, for the purpose of getting a vacuum forming machine to consistently put out parts you can use, that’s SPC, and it’s the version that does not become obsolete because it moves with the needs and the technology.
If you apply the same tools to acceptance testing of resin pellets at Receiving, it’s not SPC.
February 6, 2013 @ 9:41 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 6, 2013 @ 9:43 am
Supplier quality versus SPC:
The time frame is different. You work on arriving shipments rather than workpieces coming out of your own machines, which means you often don’t have the process sequence information and traceability is an issue. As the example of chips supplied to automotive shows, you may not have adequate technical knowledge of your suppliers’ processes. And you don’t have authority over your supplier’s employees. You may use some of the same tools, but you are tackling a different problem, and the range of actions you can take is also different.
February 6, 2013 @ 9:47 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 6, 2013 @ 9:49 am
First-hand is better than second hand. Another semiconductor company I knew first-hand made chips for automotive applications and spent ~$20M/year on failure analysis. It received failed chips from the field, chemically stripped them layer by layer down to raw silicon, took measurements and observed them with an electron microscope to identify the cause of the failure, and all of it was reported to the customer. On the face of it, it looked like an elaborate effort as solving process problems. When you looked closer, however, it became clear that the sole purpose as pacifying the customer.
By the time the chips came back from the field, four months had passed since they had been made. By the time the analysis was complete, the operation that had caused the failure had undergone two or three engineering changes, making the analysis technically pointless. Appearances may be deceiving.
The semiconductor industry is a relevant case because it uses statistical tools more than any other industry. Semiconductors and pharmaceuticals are the largest manufacturing customers of statistical software. You can check with suppliers. The pharmaceutical industry uses the tools because they are mandated for drug approval, so their use is externally driven. The semiconductor industry uses them out of technical necessity.
I have worked in other industries too, from aluminum foundries to frozen foods and car assembly, and I have never seen any realization of the vision of control charts used everywhere by operators to control processes, as advertised in the literature.
I am not swayed by your second-hand examples, because either I have first-hand knowledge of the company (Intel), they are ancient (Toyota), or unclear about actual technical content. Again, if you agree that SPC is the application of statistics to the achievement and maintenance of process capability, it doesn’t get obsolete because you are not limited to using yesterday’s technology that was developed for yesterday’s problems.
Your first-hand examples, on the other hand, are interesting. The applications you describe, however, strike me as mostly out of the realm of SPC: stocking shelves, managing inventories, triggering replenishment,… Great stuff, but it is not about getting machines to do what you want them to.
I learned Taguchi methods from his disciple Madhav Phadke in “Quality Engineering Using Robust Design.” It is useful stuff.
About PDCA/PDSA, I think both are overemphasized in the US, compared to Japan. About PDCA, you need to remember that it is an English-language acronym that I believe was made in Japan. If you consider other such acronyms, like SMED or TPM, they don’t necessarily make much sense to Americans. “Single-Minutes Exchange of Die” is not understood in the US without an explanation that “Single-Minutes” means less than 10 minutes. “Total” in TPM means with involvement by everyone, which isn’t the most common usage.
Yes, the “Check” in PDCA doesn’t sound right in English, but I am not sure that Japanese will see the nuance between the two foreign words Check and Study. Do we want to endorse and import back Japanese misuse of English? Or do we want to correct it and make an issue? With SMED, we took the first course of action; with PDSA, Deming took the other.
February 6, 2013 @ 10:05 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 6, 2013 @ 10:07 am
In Intel documents, you have references to SPC in a PowerPoint presentation and a supplier handbook.
What are you supposed to conclude from that?
Just because there is a manual, does it always mean that, when you go out to the shop floor, what you see matches what the manual says?
Have you never seen a customer organization mandate that its suppliers do things it doesn’t do?
And PowerPoint presentations always tell the truth and nothing but the truth?
What do you believe, documents or your own eyes?
This being said, a company’s documents may be half-true. They may simply embellish the truth without being outright lies. They are worth looking, at least to see the facade the company wants to present. What does the Intel presentation actually say?
The slide 5 that Dan quote as refutation of what I have been saying defines SPC as follows:
“The use of statistical techniques to analyze a process, take appropriate actions to achieve and maintain a stable process, & improve process capability.”
It seems to me to be consistent with the definition I like to use and that several of you argue against for reasons that escape me:
“In the broadest sense, Statistical Process Control (SPC) is the application of statistical tools to characteristics of materials in order to achieve and maintain process capability. In this broad sense, you couldn’t say that it is obsolete…”
And the other PowerPoint Dan pointed out to me earlier was by an Intel engineer who reported using EWMA (Exponentially-Weighted Moving Average) charts that are not part of the standard package commonly sold as SPC. I have never used EWMA charts, so I have no opinion of their usefulness. Gagandeep, however, tells me that Don Wheeler has no use for them and excludes them from SPC, making the Intel people heretics.
If you ask about cells, kanbans, andons, kamishibai, etc., it’s not difficult to google pictures of contemporary manufacturing shop floors using these techniques, massively. All I have seen on SPC in the past couple of days from this group is 50+ year-old pictures from Toyota, a reference to a speech an executive from Nashua 30 years ago, and first-hand accounts of the use of the same tools by Wayne and Dan in applications other than process control in manufacturing.
If you have been using statistical tools to achieve and maintain process capability in manufacturing operations, in the past, say 20 years, please share your experience. Details are welcome.
February 6, 2013 @ 10:26 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 6, 2013 @ 10:28 am
Thanks. I hope you don’t mind, but I have follow-up questions.
To the extent you are allowed to share this, I was wondering which operations this was on, oxidation, deposition, photolithography, etching, etc.
Were the characteristics measured inside the production equipment or on measurement instruments outside the equipment?
How was this work integrated with overall yield enhancement efforts?
Who was using the charts? Was it production operators, process engineers, technicians?
Were the charts on display all the time near the equipment, displayed only when the controller detected an event requiring investigation, or displayed on request off-line on a screen outside the fab area?
What kind of actions were taken in response to alarms?
February 8, 2013 @ 1:46 pm
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 8, 2013 @ 1:47 pm
So much for visualization, and having operators manually update charts on the line side! Some participants in this thread think it is of great value. In what you describe, all the analysis is done under the hood by software, and the responders are notified of alarms by email.
In a first phase of automation, you take a manual procedure and implement it in software. Then you realize that it gives you the opportunity to do other things that you couldn’t manually. In a second phase, you migrate from horseless carriages to cars.
Shewhart’s charts were designed to be drawn, maintained, and analyzed manually by people. The techniques used were constrained both by the information technology of the 1920s and by the need for the tools to be understood at some level by their human users. By taking people out of the data collection and analysis loop, you remove these constraints but at the same time sever the relationship between operators and the procedure.
Shewhart modeled process characteristics the sum of a constant and white noise. All the calculations are based on the assumption that the fluctuations are normal and that the measured values on all workpieces are independent. As Lasse said “something must be used,” and you decide that the discrepancies between reality and the model are negligible with respect to the objectives you pursue.
Software allows you to have a plan for every characteristic. You are not restricted to one variable at a time; you can use multivariate time-series models if appropriate. If there is autocorrelation in the process, you can use autoregression, etc. Of course, you have to know what you are doing, both statistically and in terms of process physics and chemistry. But that has always been the case. And then your system must communicate in ways that human responders can understand and act on, which is another challenge.
You don’t say whether your application is from the semiconductor industry. It is an industry of particular interest, again, because its processes are chronically out of control: the minute you have successfully brought an operation under control, you have to switch to the next generation and do it again. It doesn’t happen with shock absorbers.
In this industry, you have unit process engineers who worry about a single operation, and would use SPC in its broad sense, and you have process integration engineers who worry about the complex interactions between device characteristics determined at all operations that may make a working or a defective circuit.
The process integration part is perceived as strategic and the key to yield enhancement, and this is where most of the investments in IT and statistical tools go. The data collection for this happens at test at the end of the process, and the analysis results in tweaks at all operations, which the unit process engineers then implement.
The reasons I was given for this emphasis on process integration were (1) that the key characteristics were simply not possible to measure between operations inside the process, and (2) that subtle interactions between the 500+ operations of the process were the key. I have never heard work at this level called SPC.
Your statement that “the math hasn’t changed” is pessimistic. We have many new analytical tools since the 1920s, that we can use because contemporary IT allows us to do it.
February 8, 2013 @ 1:51 pm
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 8, 2013 @ 1:59 pm
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 8, 2013 @ 3:57 pm
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 8, 2013 @ 4:01 pm
When I say “Six Sigma people,” I mean the Master Black Belts who first explained it to me and gave a copy of Mikel Harry’s 1990 training book from Motorola University.
The idea was that having the the plus or minus 3 sigmas interval within tolerances was insufficient when faced with stackup issues with large numbers of characteristics. You needed plus or minus 6 sigmas, or 3.4 defects per million opportunities in order to have decent quality in finished products with many defect opportunities.
In this discussion, I find much use of the argument of authority. X must be true because Dr. Y said so, and I confess to using it too. It is counterproductive. Instead of exchanging technical information on what works and what doesn’t based on our own experience and thought, this turns into a scholastic debate about dogma.
As engineers, we should not accept anything as true just because anybody asserts it, no matter who it is. If the Wright brothers had done that, they wouldn’t have flown. Instead, they established through their own measurements that the published figures on lift were wrong.
@Dan – If I understand you correctly, when you say “As to empirical proof, what happened at Western Electric once Shewhart introduced his ’empirical’ limits… history is proof. ‘Ye shall know them by their fruits’,” you are attributing the business success of AT&T in the decades after 1930 to the use of Control Charts at Western Electric.
It is similar to justifying Lean/TPS by the success of Toyota. Except that, for AT&T, causality is harder to establish. Until deregulation in the 1980s, having a monopoly on the US telecommunications market might have had something to do with the company’s success.
Speaking of authorities, I was surprised when reading Out of the Crisis, that Deming thought deregulation would destroy the US telecommunications industry!
February 8, 2013 @ 4:03 pm
The whole theory of Shewhart’s control charts is based on the null hypothesis that measurements on successive work pieces are independent, identically distributed, normal random variables. You use this hypothesis to set control limits, and, with every point you add, you test the actual distribution against it. If any point is outside the limits, you reject the null hypothesis at a 0.027% level of significance.
I am not defending or attacking the theory but just stating my understanding of what it is. It sounds like classical statistical decision theory, and I just don’t understand why anybody would say that these limits are based on anything else. The question remains, however, of why use this level of significance rather than another.
If asked to justify it, I would consider the impact of false alarms, not when you are adding one point on one chart but many points on many charts every day.
Let us assume you use this technique throughout your plant and add 100 points to charts every day. Let us also assume that all your processes are and stay under statistical control, so that all the alarms you get are false. How many do you get?
Based on 3-sigma limits, the probability that none of your charts will generate an alarm in a given day is 99.73% to the power of 100, or 76.31%. It means, roughly, that you will get at least one false alarm on the average every four days.
Lower the threshold to 2 sigmas, and the probability of having no false alarm in a day drops to 95.5% to the power of 100, or barely 1%. False alarms will then be a daily occurrence, sending your responders on wild goose chases and destroying the system’s credibility.
That’s why you use 3 sigmas rather than 2. But why 3 sigmas rather than 4, 5, or 6? Every time you raise the bar, as you reduce the number of false alarms. In this hypothetical plant in a state of perfect statistical control, you could raise it as much as you want, because all the alarms you get are false…
In a real plant, however, you use the tool to detect real changes, and higher thresholds
decrease the sensitivity of your tests. With even 4 sigmas, you would miss most of the events you would actually want to catch.
I would call this a risk analysis.
If you can fit the +/- 6 sigma interval within tolerance limits,control charts are uselss.
If the measurements are not normally distributed or not independent, that is a different question, and one we have already discussed extensively. I think the key issue is the ratio of true to false alarms. If your process is in perfect statistical control, as assumed above, all your alarms are false and the control charts are a waste of effort.
The worse your process, the higher your ratio of true to false alarms, and the more useful the charts are. If it is bad enough, investigating even false alarms makes you uncover real problems.
February 8, 2013 @ 4:05 pm
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 8, 2013 @ 4:06 pm
You are correct that I was discussing only measured variables and said so when I wrote of “measurements on successive work pieces.” I didn’t want to discuss the whole array of p-charts, c-charts, and others.
As discussed before, it is the sampling distribution that needs to be normal, and CLT gives it to you approximately within a broad range and even with small sample sizes, although there are distributions for which convergence requires 1,000 values.
It doesn’t apply to standard deviations. If the underlying population is normal with independence between points, sample variances will follow a chi-squared distribution, from which you calculate a control limit for the sample standard deviation.
And it doesn’t apply to charts of individual values.
I am just describing the math he is using in terms of standard statistical decision theory. You can philosophize around it all you want, but that is the bottom line. It is how the numbers are calculated. It’s what you find under the hood. You are, of course, free to interpret them as you see fit. In Gagandeep’s Wheeler quotes, I only see assertions, but no argument.
February 11, 2013 @ 10:20 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 11, 2013 @ 10:24 am
I agree with you that this thread is bizarre. I am also surprised by the large number of posts, by the confusion they reveal, and by the unusual resort to the argument of authority. It is more like a 16th century theological debate than a 21st century discussion of how to make products with consistent characteristics.
I think it reveals that, while elegant, SPC is neither simple nor easy to understand. From your profile, I see that you have spent almost 20 years in the food industry, which has its specific quality challenges, like making products that taste the same in spite of variability in the ingredients, or freshness issues… And I am sure you have plenty of ideas on how to address them.
You feel that all the high-level computer hardware and software paraphernalia is unnecessary, and I’ll take your word for it in food processing. That does not prevent it from being indispensable in other industries, like semiconductors.
You ask how you can make sensible use of this vast arsenal, which can be very useful, when you don’t understand the “simple, elegant and time-tested principles” that underlie SPC. To me, it’s like saying that you can’t understand computers unless you know how to use a slide rule.
Using modern tools requires many skills, that only have a minor overlap with the old ones. You need to know how to locate errors in databases and filter or correct defective data. Then there are challenges in deciding which analysis tools to use, how to interpret the results, and how to communicate your conclusions.
You are describing a situation among your clients where they have lost the old skills, not learned the new ones, and are clueless as to what their needs are. It seems you have plenty of work to do.
February 11, 2013 @ 10:32 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 11, 2013 @ 10:35 am
What Shewhart says of empirical evidence is true of any kind of data analysis. If we pay attention to Nate Silver, it’s not for his mastery of bayesian theories but for his ability to predict election results with great accuracy.
There are three levels to any system that deals with data. The first is the way it looks to people or machines that interact with it, including what input it receives and in what form, and what output it produces: charts, flashing lights, automatic adjustments, etc.
The second level is its internal logic, the model it is based on and how its diffferent components interact. This is where distributions and risk calculations reside.
The third level is the way it maps to external reality: how effectively it addresses the problem it is intended to solve.
This is nothing special to SPC. In manufacturing, you have to address these issues in Production Control or Maintenance as well as in Quality. And you do in airline reservation systems too when you use models of no-shows to overbook flights with the goal of filling planes without denying seats to any passenger with a reservation.
Why do you say that p-charts limits are distribution-free? The formula you give is for a null hypothesis that the percentage defective follows the normal approximation of a binomial distribution.
February 11, 2013 @ 10:38 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 11, 2013 @ 10:41 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 11, 2013 @ 10:43 am
In the accounts both from Lasse and Drew, Control Charts are neither posted on the shop floor nor used by production operators but instead used for automatic alarm generation, with the alarms passed by email to process engineers who view the charts on demand on computer screens.
This is fundamental, because it is consistent with the traditional view of quality as being the job of specialists rather than involving everyone, as opposed to Art Smalley’s example from the 1950s at Toyota that Dan pointed out. (http://bit.ly/WTxpdx).
It means, that, whatever their job title may be, there is a group of responders in the plant organization, tasked with acting on alarms generated by control charts. This may mean stopping the machine, putting together a problem-solving team, running tests and experiments on the machine, and implementing both immediate countermeasures and long-term solutions.
To manage how the responders’ group performs and how large it should be, you cannot just consider what happens when you add one point to one chart but instead the consequences of having multiple charts routinely updated within the plant, all of which generate alarms that this group must respond to.
The average run length (ARL) parameter Gagandeep describes is indeed useful, but it should be clear that it is the mean number of points between FALSE alarms. When you look at the probability of a point being within 3 sigmas of the mean, 98% looks close to 99.73%, and that is the reason Gagandeep says that departures from normality in the underlying distribution are not a problem. When you look at ARLs, however, the picture is different.
As Gagandeep pointed out, the 99.73% figure corresponds to ARL = 370, meaning that you have one false alarm every 370 points. On the other hand, a distribution with only 98% of the points within 3 sigmas of the mean will give you a false alarm on the average every 50 points, about 7 times more often! This is not a minor difference.
How important are false alarms? Their absolute number is not the issue. What really matters is the ratio of true to false alarms. If, as in semiconductors, your processes are chronically out of control, you may get, say, 10 true alarms for every false alarm. And your processes are so unstable that even an investigation launched on the basis of a false alarm is likely to provide real improvement opportunities.
If, on the other hand, you have processes that are as mature and stable as drilling, the picture is different. I was suggesting earlier the thought experiment of a process that NEVER goes out of statistical control. Based on the ARL, it will still generate alarms, and they will be ALL false and sending the responders on wild goose chases. It is like testing a population for a disease that none of its members has. Since tests are not perfect, some will come out positive, and the positives will be all false.
In a real manufacturing situation, not only Control Charts but even more modern statistical methods lose their effectiveness when you are so close to statistical control that lack of process capability is no longer the main source of defects.
Rather than a drift in mean or spread in a measured characteristic, your defects are then caused by discrete events like tool breakage or operator errors. That is the point where one-piece flow with go/no-go checking take over, followed by mistake-proofing.
February 11, 2013 @ 10:44 am
@Gagandeep – You seem to be forever parsing Shewhart’s words. The way the same material in math, science, or technology is explained evolves over time. I could find no occurrence of expressions like “null hypothesis” or “level of significance” in his writings. Yet, in the way I was taught the subject 40 years later, these are central concepts that support clear and concise explanations of methods, including Shewhart’s control charts.
I suspect that, when he was writing in the 1930s, the general framework of statistical decision theory either didn’t exist yet or was just emerging. It would explain why he didn’t use it. I am sure he meant something by “probability limit,” but I have no idea what, and the expression makes no sense to me.
And, frankly, I have a hard time with the idea that it makes any difference to manufacturing quality in 2013.
February 11, 2013 @ 10:46 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 11, 2013 @ 10:51 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 11, 2013 @ 10:53 am
@Gagandeep –
You quoted Deming saying: “Rules for detection of special causes and for action on them are not tests of a hypothesis that a system is in a stable state.”
How does this make any sense? Obviously, when you are applying a rule, you are doing a test.
You also quote Wheeler saying: “Shewhart’s approach to the analysis of data is profoundly different from the statistical approach.”
Then why does Shewhart call his book “STATISTICAL Method from the Viewpoint of Quality Control”?
I don’t see anything wrong with transforming data to make it talk. You do it all the time when you show scatter plots with semi-logarithmic or bi-logarithmic axes. The commonly used lognormal distribution is DEFINED by the logarithms of a variable being normal. You also transform time or space series in more complex ways when you calculate power spectra.
February 13, 2013 @ 11:22 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 13, 2013 @ 11:24 am
As I understand what you are saying, knowledge of the process is necessary to interpret the data it puts out and make sensible predictions. It is true for manufacturing processes, but it is also true in every domain whenever you are trying to use data on the past and present to predict the future, whether you are talking about sales, baseball scores, or the weather.
You will not get anywhere by applying statistical algorithms without understanding the dynamics of the domain. When statistics works, it is always as an add-on to domain knowledge, never as a substitute to it.
As for “probability limits,” again, I don’t know what it means, but I can think of one analysis technique that is still in use today and was invented without any recourse to probability theory. Candlestick charts are still used by stock traders, mostly in Japan. They were invented in 18th century Japan by rice trader Munehisa Honma, who also invented futures trading, made a fortune and lived a long life. He based trading decisions on patterns observed in Candlestick charts. It was purely empirical.
February 13, 2013 @ 11:30 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 13, 2013 @ 4:13 pm
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 14, 2013 @ 9:01 am
Ronald Fisher‘s Studies in Crop Variation from the 1920s were actually the basis for his development of many of the classical tools of statistics, in particular analysis of variance (ANOVA) and design of experiments (DOE).
In making predictions, probability theory and subject matter expertise are not mutually exclusive but complementary, with probabilistic models helping you avoid biases and quantifying risks. And probability theory is not always needed. A molecular biologist who was renowned as an experimenter once told me that she had never heard of DOE. The outcomes of her experiments were binary: either a result was there or it wasn’t.
Agriculture as a domain is much more variable than anything we deal with in a lab or in manufacturing. Differences in, as you say, soil; weather; planting, growing, and harvesting techniques cause variations that may dwarf the impact of seed choice. In addition, agriculture is an intrinsically batch process: you plant your seeds, watch them grow for months, and then harvest the whole crop in a few days.
This means that it can take a year before you can measure the results of an experiment. In your example, if you wanted to make sure that your choice of fields in Washington did not influence the outcome, you would need to switch seeds between the fields and grow another crop, which would take another year. Then, to make sure it wasn’t the influence of the weather, you would have to grow the crops enough times to filter it out… After 10 years, you might be sure.
By contrast, in a machine shop, you work with variations on the order of 1 mil on dimensions in multiple inches, in the controlled environment of a factory, with the well-known physics of metal cutting, and with process times for single workpieces measured in seconds for automotive applications and, at worst, in weeks in aerospace, which means cycles of learning that are orders of magnitude shorter than for agriculture.
It is not necessarily a simpler challenge, but it is a different one, for which Shewhart developed specific statistical tools, and Shingo later non-statistical tools for more mature processes.
Once you complete a process capability study on a machine, you use the results as a basis for control on this machine. That’s the whole point of the study. But what about using the same parameters on other machines? That they apply is your null hypothesis; if your controls refute it, then you conduct another study on the new machine.
February 21, 2013 @ 5:42 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 21, 2013 @ 5:43 am
Whatever works… What I don’t understand is why you would not use subject matter expertise to understand the past, and why you would not use probability to predict the future.
February 21, 2013 @ 5:45 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 21, 2013 @ 5:53 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 21, 2013 @ 5:55 am
You wrote: “… the math used to calculate the mean and the standard deviation may come from probability theory but where the limits are placed does not…”
The logic of that statement escapes me.
Some understanding of methematical statistics is necessary, and the absence of this knowledge in manufacturing organizations has severely limited the diffusion of these methods, the Black Belt system being an attempt to fill this gap.
Attempts to apply these tools without the requisite knowledge result in mistakes like checking averages against limits set for individual values.
As for transformations, your “raw” data is already usually a voltage tranformed by software into a length, emperature, weight, decibels, etc. Some further transfomations may be perfectly valid, if you know what you are doing. I understand this is a big “if.”
February 21, 2013 @ 5:58 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 21, 2013 @ 5:59 am
The application of probability in question here is statistical decision theory. It has been developed specifically for situations in which you don’t have perfect knowledge and must approximate.
The range of probabilities of not having a false alarm whenever you add a point has been quoted earlier in this thread as being between 98% and 99.73% for a range of distributions. As I have explained earlier, it is not a small range when you consider not one point but 50 or 100 different points added to charts and checked against limits every day.
I don’t know why you keep bringing up “high speed,” when the determining factor for the relevance of statistical tools to quality improvement is not speed but technology. Making and packing detergent powder is high-speed manufacturing; fabricating state-of-the-art integrated circuits, high technology.
In mature processes, capability is not an issue, and the statistical tools are ineffective. That is why you see plants producing top quality auto parts that don’t have a single employee trained in statistical tools. Quality enhancement at this level is pursued by non-statistical tools, like one-piece flow, stop ropes, andons, go/no-go gauges, mistake-proofing, JKK,…
In high technology, where processes are always immature, you need statistical tools, but the old SPC can’t cut the mustard. As Lasse and Drew pointed out, measurements on individual operations are automatically collected and analyzed, with specialized responders for software-generated alarms that are nowadays based on more advanced methods than Shewhart’s, as your Intel 2006 article indicated.
From my own experience of the industry, whatever you do on individual operations is necessary but minor. What determines yield is the integration of hundreds of operations in a process whose outcome cannot be seen until it is finished. And the yield enhancement groups are using much more sophisticated tools than SPC.
Browsing through a just published handbook of quality management, I was struck by the absence of any discussion of the range of applicability of the various tools described. In addition, this book fails to cover the methods used by the few companies that are actually able to make 1 million units of product without a single defective.
February 21, 2013 @ 6:01 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 21, 2013 @ 6:02 am
Sometimes, entire professions get so wrapped around their own dogmas that they lose touch with reality. It happened to management accountants in the 1980s. They were so attached to techniques developed in the 1910s at Dupont that they failed to see how irrelevant they had become. They did things like give you unit costs that were calculated by Materials, Labor, and Overhead, in which the Overhead category was 90% of the total.
They got wake-up calls from some of their own, like Robert Kaplan, but also from outsiders like Eli Goldratt. And, since then, there have been several efforts to update the field, from Kaplan’s Activity-Based Costing and Goldratt’s Throughput Accounting to Brian Maskell and Orrie Fiume’s Lean accounting.
When I look at the literature from the American quality establishment, or the program of courses offered by the ASQ, I see a similar situation. In cars, the J.D. Power and Associates Initial Quality Survey for 2012 has Toyota and its Lexus and Scion brands back at or near the top in most categories. Incidentally, Honda/Acura is not far behind, and, in some categories, ahead. Such results should make the quality profession curious about the quality side of the Toyota Production System, but it doesn’t act interested.
The methods to achieve these results are not secret. They can be learned. More than 10 years ago, Kevin Hop and I developed a course on Lean Quality that was well received, … in China. But these methods are not statistical. You don’t need to know them in order to pass a certification exam, ISO-900x audits, or receive the Macolm Baldridge Award.
There are other elephants in the Quality room that the profession seems to be ignoring. The 2001 Firestone tread separation debacle, or the 2010 Toyota recalls should make it clear that a major part of quality management is emergency response. When such events happen, quality managers have to step in with immediate countermeasures, organize the search for permanent solutions, and communicate about their actions with customers and the media. I could not find a word about this in the latest Handbook for Quality Management. The word “recall” is not in the index. On the other hand, you have several pages on Maslow’s hierarchy of needs.
Unlike Shigeo Shingo, I am not saying we should get rid of statistical tools in quality engineering and management. I think instead that we should use the right tools where they apply, whether they are statistical or not.
If you juxtapose quotes from Mikel Harry and Shigeo Shingo, you have the appearance of irreconcilable differences, until you realize they came from radically different industrial backgrounds, and that each one was expressing as universal truths statements that applied to specific and different contexts.
February 21, 2013 @ 6:08 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
February 21, 2013 @ 6:09 am
In the most classical SPC model, you start by doing a Process Capability Study, during which you take measurements of a quality characteristic that you deem representative of normal behavior. It’s a judgement call, but it often involves excluding outliers.
You then estimate the mean and standard deviation of the characteristic from this sample, and use these parameters to set Control Limits based on standard formulas.
Implicitly, what you are doing is fitting a probabilistic model to your data, and this model is that the characteristic follows a normal distribution, and that the sequence of measurements are independent and identically distributed (i.i.d.). It is implicit, because the literature doesn’t say so, but all its calculations are based on it.
What you do afterwards when you plot your Control Charts is not assuming that this model remains valid but instead using it as a null hypothesis that you test against. What every limit crossing is telling you is that the model no longer applies.
What determines the usefulness of the tool when you use it systematically, day in and day out on a factory floor is the ratio of real to false alarms that it produces. If, the process is unstable, you will get many real alarms and the tool will be useful. On the other hand, if the actual process fits the model perfectly all the time, you will have nothing but false alarms and the tool will be useless.
Why were Control Charts used at Toyota in the early 1950s? Because the processes were unstable.
Why, as Art Smalley reports, did Toyota stop plotting Control Charts 30 years ago? Because its processes were so stable that the charts were useless. They were actually worse than useless, because they started people chasing non-existent causes.
Providing probabilities for future events is the whole purpose of probability theory.
Having stable processes does not mean that your products are defect-free, only that the defects are not caused by drifts in your processes. Discrete-events like sudden tool failures and human errors still remain; the Lean approach to progress further is to use tools like one-piece flow, go/no-go gauges, and mistake-proofing that are not statistical in nature.
The quality characteristics of a part coming out of an operation over time are a time series, and there are time series models in multiple dimensions that can represent, for example, correlations between characteristics of the same part, and autocorrelations between them over time. The EWMA (Exponentially Weighted Moving Average) that Dan quoted as used at Intel is an example of such a tool.
Shewhart couldn’t use such tools because they didn’t exist in 1931 and neither did the technology to make calculations based on them. Had they been available, he might still have chosen not to use them, as being impossible for his manufacturing audience to understand. But then, in the ensuing 82 years, even his Control Charts have been widely misunderstood.
February 21, 2013 @ 6:13 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
Standards and Opportunities for Deviation | Michel Baudin's Blog
November 6, 2013 @ 9:54 pm
[…] of the quality profession in the US still promote as a standard the 80-year old tools of SPC, as if the art of collecting and analyzing data had not evolved since 1930. These tools are […]
Why Your Lean and Six Sigma Improvement Efforts Aren’t Driving Better Results | IndustryWeek | John Dyer | Michel Baudin's Blog
May 28, 2015 @ 9:56 am
[…] author opens with SPC control charts, which aren't even part of Six Sigma as originally developed. These control charts […]
Productivity and Technology | Michel Baudin's Blog
June 20, 2017 @ 11:12 am
[…] Statistical Process Control, as taught today, is still based on 90-year old techniques tailored to the age of mechanical […]
October 12, 2017 @ 2:32 pm
Ever since asking Is SPC Obsolete? on this blog almost 6 years ago, I have been told from multiple sources that the X-mR chart is a wonderful and currently useful process behavior chart, universally applicable, a data analysis panacea, and requiring no assumption on the structure of the monitored variables. So I dug into it. Here is an example of what these charts look like:
The top chart shows individual measurements over time; the bottom one, a moving range based on the last two values. What makes this more than a plain times series charts — the likes of which are found in as unsophisticated a publication as USA Today — is the red dashed lines marking control limits.
Misleading time series from USA Today
The method for setting these limits is therefore essential to the tool, and it is based on multiples of the average of the moving range . What the literature tells you is that, for the chart of individual values, the limits are at:
. What the literature tells you is that, for the chart of individual values, the limits are at:
and for the range at
The readers are discouraged from worrying their heads with the provenance of these numbers, and the closest they get to an explanation is a reference to a table where such coefficients are kept, and this table was generated by a higher authority. No further explanation is found books by Douglas Montgomery, J.M. Juran, or Don Wheeler.
The assertion that these numbers are valid regardless of the data’s variation pattern strains credulity. Clearly, they did not come out of thin air. There is a theory behind them, that theory is based on assumptions about the data, and it is necessary for users to know these assumptions so that they can understand the domain of applicability of the technique, with its blurry boundaries. You may still get some use out of the technique when the conditions are not fully met, but you should do so knowingly. As discussed in an earlier comment, chemical engineers commonly apply formulas for perfect gases to gases they know aren’t perfect.
Not finding this information for the X-mR chart, I undertook to work it out myself, starting with the model implicit in the SPC literature, that a process variable X is the sum of a constant C with a white noise W. Formally, for the i-th measurement,
where the are independent Gaussian (a.k.a. “Normal”) variables with 0 mean and standard deviation σ. Let us consider the differences between consecutive variables
are independent Gaussian (a.k.a. “Normal”) variables with 0 mean and standard deviation σ. Let us consider the differences between consecutive variables  and
and 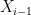 :
:
As sums of two independent Gaussian variables with 0 mean and standard deviation σ, they are also Gaussian, with 0 mean and standard deviation . The range
. The range 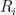 is the absolute value of this difference:
is the absolute value of this difference:
and follows the folded Gaussian distribution, with formulas for mean and standard deviation that simplify as follows when the Gaussian being folded has 0 mean. The mean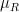 of the range is:
of the range is:
and therefore:
which results in:
For the standard deviation of the moving range, we have:
of the moving range, we have:
This means that, for R, the 3σ upper control limit is:
This derivation confirms that the published coefficients are based on the assumption that the monitored variable is Gaussian. Of course, it doesn’t prove it but it is highly unlikely that any other distribution would produce the exact same coefficients.
Is SPC Obsolete? (Revisited) | Michel Baudin's Blog
December 10, 2017 @ 12:33 pm
[…] years ago, one of the first posts in this blog — Is SPC Obsolete? — started a spirited discussion with 122 comments. Reflecting on it, however, I find that […]
The Math Behind The Process Behavior Chart - Michel Baudin's Blog
March 2, 2019 @ 7:49 am
[…] since asking Is SPC Obsolete? on this blog almost 6 years ago, I have been told from multiple sources that the X-mR chart is a […]
Process Control and Gaussians
March 5, 2024 @ 11:38 am
[…] Is SPC obsolete? (2011) […]