Jul 23 2012
Safety Stocks: More about the formula
In a previous post on 2/12/2012, I warned against the blind use of formulas in setting safety stock levels. Since then, it has been the single most popular post in this blog, and commands as many page views today as when it first came out. Among the many comments, I noticed that several readers, when looking at the formula, were disturbed that three of the four parameters under the radical are squared and the other one isn’t, to the point that they assume it to be a mistake. I have even seen an attempt on Wikipedia to “correct that mistake.”
I was myself puzzled by it when I first saw the formula, but it’s no mistake. The problem is that most references, including Wikipedia, just provide the formula without any proof or even explanation. The authors just assume that the eyes of inventory managers would glaze over at the hint of any math. If you are willing to take my word that it is mathematically valid, you can skip the math. You don’t have to take my word for it, but then, to settle the discussion, there no alternative to digging into the math.
A side effect of working out the math behind a formula is that it makes you think harder about the assumptions behind it, and therefore its range of applicability, which we do after the proof. If you don’t need the proof, please skip to that section.
Contents
Math prerequisites
As math goes, it is not complicated. It only requires a basic understanding of expected value, variance, and standard deviation, as taught in an introductory course on probability.
In this context, those who have forgotten these concepts can think of them as follows:
- The expected value E(X) of a random variable X can be viewed, in the broadest sense, as the average of the values it can take, weighted by the probability of each value. It is linear, meaning that, for any two random variables X and Y that have expected values,
and, for any number a,
- Its variance is the expected value of the square of the deviation of individual values of X from its expected value E(X):
Variances are additive, but only for uncorrelated variables X and Y that have variances. If
then
- Its standard deviation is
Proof of the Safety Stock Formula
Fasten your seat belts. Here we go:
As stated in the previous post, the formula is:
Where:
- S is the safety stock you need.
- C is a coefficient set to guarantee that the probability of a stockout is small enough.
- The other factor, under the radical sign, is the corresponding standard deviation.
- μL and σL are the mean and standard deviations of the time between deliveries.
- μD and σD are the mean and standard deviation rates for the demand.
is the standard deviation of the item quantity consumed between deliveries, considering that the time between deliveries varies.
μD and are the mean and variance of the demand per unit time, so that the demand for a period of length T has a mean of
, a variance of
, and therefore a standard deviation of
. See below a discussion of the implications of this assumption.
Note that the assumptions are only that these means and variances exist. At this stage, we don’t have to assume more, and particularly not that times between deliveries and demand follow a particular distribution.
If is the demand during an interval of duration T, since:
we have:
If we now allow T to vary, around mean μL with, standard deviation σL , we have:
and therefore:
and
That’s how the variance ends up linear in one parameter and quadratic in the other three!
Then:
QED.
Note that all of the above argument only requires the means and standard deviations to exist. There is no assumption at this point that the demand or the lead time follow a normal distribution. However, the calculation of the multiplier C used to set an upper bound for the demand in a period, is based on the assumption that the demand between deliveries is normally distributed.
Applicability
The assumption that the variance of demand in a period of length T is implies that it is additive, because, if
, then
.
But this is only true if the demands in periods and
are uncorrelated. For a hot dog stand working during lunch time, this is reasonable: the demands in the intervals between 12:20 and 12:30, and between 12:30 and 12:40 are from different passers by, who make their lunch choices independently.
On the other hand, in a factory, if you make a product in white on day shift and in black on swing shift every day, then the shift demand for white parts will not meet the assumptions. Within a day, it won’t be proportional to the length of the interval you are considering, and the variances won’t add up. Between days, the assumptions may apply.
More generally, the time periods you are considering must be long with respect to the detailed scheduling decisions you make. If you cycle through your products in a repeating sequence, you have an “Every-Part-Every” interval (EPEI), meaning, for example, that, if your EPEI is 1 week, you have one production run of every product every week.
In a warehouse, product-specific items don’t need replenishment lead times below the EPEI. If you are using an item once a week, you don’t need it delivered twice a day. You may instead receive it once a week, every other week, every three weeks, etc. And the weekly consumption will fluctuate with the size of the production run and with quality losses. Therefore, it is reasonable to assume that its variance will be where T is a multiple of the EPEI, and it can be confirmed through historical data.
You can have replenishment lead times that are less than the EPEI for materials used in multiple products. For example, you could have daily deliveries of a resin used to make hundreds of different injection-molded parts with an EPEI of one week. In this case, the model may be applied to shorter lead times, subject of course to validation from historical data.

July 23, 2012 @ 5:06 pm
Okay Michel . . . I got lost in (or bored with) the math. If you’re customer-focused, I agree with the need for safety stock. What I think is critical, though, is that, even though it may be needed given current circumstances, to never NEVER think that safety stock is acceptable. I’ve seen companies way too often use formulas to determine safety stock, EOQ, etc. and stick with them for years without ever questioning why they need stock at all.
I agree with you on your point regarding the need to understand “assumptions.” Unless the data follows a normal distribution, average and standard deviation are meaningless. And the last time I checked, the data in most companies does not follow a normal distribution.
Great post! Keep them coming!
Gregg Stocker
July 23, 2012 @ 10:54 pm
I hear you, and I wouldn’t have described how this formula arises if so many people hadn’t been assuming it’s a typo. If you are willing to take my word that it is not, you can skip the math. No one has to take my word for it, but then, whoever doesn’t has to read the math.
There is a whole zoo of distributions other than the Normal with well-defined and meaningful means and standard deviations, including Uniform, Bernoulli, Binomial, Negative Binomial, Exponential, Poisson, Lognormal, Beta, Gamma, Weibull,… If you have data that doesn’t follow a Normal distribution, there are many other models that can be useful.
July 26, 2012 @ 9:42 pm
Michael,
The formula you quote is the popular one quoted and used in numerous texts and IT programs like visual manufacturing. I believe that there are much simpler and more effective ways of controlling stock levels than this. All that is needed is a very simple formula linking the amount shipped to the lead time for replacement and the batch size for economic supply with a safety factor simply related to the cost of the risk of non supply. A knowledge of probability theory and frequency distributions is not required but you can add to this the standard deviations if you like. However, if the frequency of delivery and the uncertainty is due to a poor supplier or poor supply chain you are far better off forming a team and eliminating the normal long lead time forecasting techniques and substituting a replacement based on stock movements. I have used these simple ideas very effectively for companies from $300M to $7M turnover. Some of the results of these simple ideas are discussed in my latest book, but I do not include the maths. These formulae have not been published but if there is enough interest I may publish these in our journal, “New Engineer”. They were vetted and supported some time ago by Prof Kenny Preiss from Ben Gurion University.
Supermarket sizing | Michel Baudin's Blog
February 18, 2013 @ 4:42 pm
[…] For details on pull systems, see Lean Logistics, Part IV, pp. 197-330. See also the two posts on Safety Stocks: Beware of Formulas and Safety Stocks: More about the formula. […]
June 23, 2014 @ 1:22 am
Micheal,
I haven’t understood your demonstration in the part where: E[D^2]=E[E[D(t)]], i knew the expected value of an expected value is the second itself (the expected value of a costant is the costant).
I found on books that, with x and y indipendent: Var(X*Y)=var(X)*var(Y)+var(X)*E(Y)^2+var(Y)*E(X)^2.
So, in this case, should be:
Var (d t)=Sd^2*Sl^2+Sd^2*ml^2+Sl^2*md^2
And SS=k*(Sd^2*Sl^2+Sd^2*ml^2+Sl^2*md^2.)^1/2
Why the formula for the safety stocks isn’t the one above?
Thank You
June 23, 2014 @ 7:02 am
I only included the proof of the formula because so many people think there is an error in it. I am sorry you are having trouble following it, but I really don’t want to get into more details of the proof.
Whether you are intellectually comfortable with the proof is really not the issue. My key point, however, was not that you should use the “right” formula for safety stock, but that you be wary of relying on any formula.
If a formula exists and is given in textbooks, it is quite tempting for a practitioner to just use it without asking any further questions. In fact, whether about gases or safety stock, a formula is valid only as part of a mathematical model of the phenomenon, and, before plugging the formula into your spreadsheets, you should always ask whether the model fits your specific situation.
November 11, 2014 @ 5:31 am
Hi Michel
Thank you so much for the post. Is there published documentation on this proof. I would like to go into the math in a little bet more detail to expand my own understanding. I work with a variety of different situations where one safety stock formula doesn’t fit all. Are there any sources you could recommend that go into more detail?
November 11, 2014 @ 6:10 am
Perhaps you could check David Simchi-Levi’s The Logic of Logistics, but you may not find it an easy read.
The proof above is not from any book. Most books on inventory are targeted to math-phobic readers and just quote the formula without proof. However, it’s not that complicated, and I worked it out on my own.
September 17, 2015 @ 3:29 pm
Instead of using the Normal distribution, why not use the kernel density of the lead-time demand sample?
September 17, 2015 @ 6:42 pm
I suppose you could do it. I don’t think kernel density estimation (KDE) was available at the time the formula was worked out. You would then have to use quantiles of the estimated density instead of a multiple of the standard deviation.
I might recommend doing that if I recommended using the formula, which I don’t.
November 11, 2015 @ 2:43 am
This is the one and only derivation of this formula that I have been able to find through Google! In my attempt to comprehend this complex situation, would you kindly confirm if the Units of variance of the demand are (demand/time)^2 Or demand^2/time? The confusion arises since the units of standard deviation of demand per time-unit would be demand/time and hence variance should have the units of (demand/time)^2 but that would make the formula inconsistent.
March 21, 2016 @ 2:05 pm
Remember that, for independent random variables, the variance of the sum is the sum of the variances, but the standard deviation of the sum is NOT the sum of the standard deviations.
That’s why the variance of the demand during a time interval of length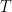 is
is
March 21, 2016 @ 1:12 pm
@Mahit I struggle with the same point you brought up. In dimensional analysis, the units should be consistent to be additive. I know I may be missing something.
August 21, 2018 @ 7:43 pm
I agree with Michel that the blind use of this formula is probably a bad idea. I also wrote up my own derivation for those interested. Hit me up if you want to discuss!
SS formula derivation:
https://math.stackexchange.com/questions/2883010/derivation-of-the-safety-stock-formula-on-wikipedia
January 25, 2022 @ 12:15 am
Technically this formula is incorrect – dimensional analysis is used by engineers and scentists to check formula validity by expressing each part of a formula in terms of the fundamental units Mass, Length and Time. The formula proposed here cannot be right because two parts with different dimensions are added together and this is cannot be correct!!
Practically the formula seriously under-estimates the necessary safety stock for two reasons:
1 – Demand distribution – with higher levels of demand variance because the demand is not nromally distributed – it cannot go below zero.
2 – Lead times are not normally distributed either – when a disruption causes lead time to exceed the planning lead time supply orders will queue so there will be several consecutive orders that are delayed.
For a better model visit https://safetystock.guru
January 25, 2022 @ 5:07 am
It’s not my formula. I didn’t come up with it and, when I first saw it, I had the same reaction that it wasn’t homogeneous. I had to work out the math to realize that, with the right assumptions, it is in fact mathematically correct.
This being said, it doesn’t mean that, in practice, it is a good way to set safety stocks. The main point of my two posts about it is that it’s not, because its assumptions are rarely satisfied.
February 14, 2022 @ 6:39 am
I think the mus lose their units; they are dimensionless.
February 14, 2022 @ 1:58 pm
Didn’t have time to go through the math before the last post, and of course this was irking me. The “T” is what is unitless as the duration is wrapped up in the demand piece itself. T is an input to that demand function. This means the L subscript terms are unitless in the formulation, and the D subscripts have the unit of concern.