Mar 19 2013
Replenishment lead time in retail
Raj Govindarajan asked the following question:
Your blog on Safety Stock Formula was very fascinating. I work in a Retail company and I am trying to apply the safety stock formula to the retail environment. Is it fair to consider “Replenishment Intervals” as “Lead Time”? In other words, for example, I have a lead time of 7 days, but I order every day to the store; so should I consider demand variability for 7 days or 1 day?
As you may recall, I am advocating wariness in applying the formula. If you are ordering every day for delivery 7 days later, you are not using the reorder point logic the safety stock formula is based on. With a reorder point, you are only placing an order when your stock crosses a threshold, and the stock on hand at that time is supposed to carry you until the order is delivered.
The question you are faced with, for each item, is “How much do I need to order today to make sure I don’t run out 7 days from now?” The elements you have to make that decision are as follow:
- The quantity on hand you have today.
- The already ordered quantities that will be delivered in the next six days.
- Your sales forecast, with confidence interval, for the next seven days.
The tricky part is the sales forecast. The safety stock formula assumes a consumption rate that fluctuates around a constant mean. This may not fit your products. To check it out, you need to analyze sales history. Cell phones and artichokes are both retail products, but with different demand structures.
For your products, you need to know whether they are on a trend that is long-term compared to 7 days, and which kind of trend. In addition, is there a weekly pattern in sales? Do your products sell more, or less, on week-ends? Data mining on your sales history can give you the minimum on hand you can expect at the end of six days and the quantity you need to receive on the seventh to avoid running out.
And you have to keep in mind that these calculations are only valid in the absence of earthquakes, hurricanes, stock market crashes, wars breaking out, new product introductions, or any other event that can severs the connection between historical data and the near future.
March 20, 2013 @ 1:05 pm
Just for the calculation of the buffer, I would recommend using the 7 days (imagine 7 days above or below average, so not hovering around average). When, however, during the response time there is little cumulative deviation – so demand is random around the average – buffering for the interval is enough. Cycle stock ,in either case, will be based upon the delivery interval, not the response time of 7 days.
Best regard,
Rob van Stekelenborg
March 20, 2013 @ 2:06 pm
Raj didn’t say whether he was talking about calendar days of business days. I am assuming calendar days for the sake of simplicity: the retail store is open 7 days a week, and deliveries occur every day.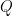 and on order
and on order  . If it is not enough to meet the demand during that period, you are out of luck.
. If it is not enough to meet the demand during that period, you are out of luck.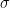 around a constant daily mean
around a constant daily mean 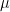 , then the mean demand for six days will be
, then the mean demand for six days will be 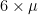 , but the standard deviation for six days will be
, but the standard deviation for six days will be 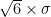 .
.



In the way Raj explained the situation, the die is cast for the next 6 days. All you are going to have to sell is what you already have, the quantity on hand
The key thing to remember when calculating the worst-case scenario for your stock at the time your next order is delivered 7 days from now is that, while means are additive, extreme values are not.
Assuming you have independent daily fluctuations with standard deviation
Then, as a confidence interval for the quantity in stock when your next order arrives, you can use:
Then, to make sure you don’t run out on the 7th day, you need to order:
And you don’t have to use a multiplier of 3 for the standard deviation. Whatever number you use depends on how high a risk of shortage you are willing to accept. It won’t be the same for a candy item and for a vaccine.
You can’t use this kind of reasoning for products with a rapidly rising demand, like a popular toy, or a recurring weekly pattern in sales, where, for example, you sell 50% of the weekly total just on Saturdays. But you probably can with rice, milk, or sugar.
March 20, 2013 @ 3:50 pm
Thanks for your further elaboration. I agree with the fact means are additive and random variations will cancel each other out.
One other remark. I noticed you spoke about safety to buffer forecast inaccuracies. Now that is the common practice when in push flow mode.
In pull flow, however, I always only look at variation in real consumption. Consumption variation typically is far less than forecast inaccuracy. Also because in forecast inaccuracy you have (severe) errors in the estimate of the mean that translate into “variation” in the formulas, and not -like with consumption- only variation around the known mean. Another great advantage of pull flow.
March 20, 2013 @ 6:29 pm
Using pull in this context would mean ordering today the quantity that you sold today, and it is tantamount to forecasting that you will sell 7 days from now the same quantity that you did today.
There are two issues we should keep in mind:
That is why I am recommending doing more data mining in the sales history.