Apr 24 2014
Learning and Experience Curves in Manufacturing | Quarterman Lee
See on Scoop.it – lean manufacturing
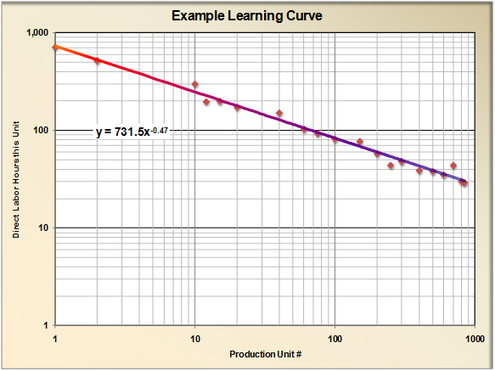
The learning curve came into prominence during World War II when Army Air Force scientists noticed that the cost for a given aircraft model declined with increased production in accordance with a fairly predictable formula. Each time the cumulative production doubled, cost declined by a fixed percentage. In the aircraft industry, at that time, this reduction was about 20%. Learning curves underpin the concept of Continuous Improvement.”
It’s good to see a well-documented, informative article by Quarterman Lee on a topic that is often ignored in the Lean literature but that I think if fundamental to the economics of improvement.
The title mentions both Learning and Experience Curves, but the body of the article is only about Learning Curves. The difference between the two is that Learning Curves are only about labor, and were developed first, in World War II, as Quarterman points out. The Experience Curve is a generalization due to Bruce Henderson of the Boston Consulting Group in the 1960s, which applies the logic not just to labor but to all costs.
The Experience Curve theory is predicated on the notion that there is such a thing as a meaningful cost per piece, and asserts that it decreases with cumulative volume along an inverse power curve, the evidence for which is in the evolution of market prices with cumulative volume in a variety of industries.
The effect of this curve on pricing in an industry depends on its clockspeed. In electronics, with product lives of four years, it is dominant. In cars, where the experience accumulated for over a century is still relevant today, we are so far on the curve that it is not a major factor.
The justification for an inverse power law is in fact simple. It stands to reason that, the more you have already made of a product, the easier it is to make the next unit, and therefore that costs should decrease as a function of cumulative volume. Since we are talking about a broad trend, it should also be a smooth decline.
Could it be linear? No. It would mean a straight line in cartesian coordinates.and that would lead to negative costs, which makes no sense. If you toggled the y-axis to “logarithmic,” a straight line would represent an exponential decline. But it would not make sense either, because it would mean that you could produce an infinite volume for a finite cost. If, as in the above picture, you make both axes logarithmic, a straight line means an inverse power law. Costs never go negative, and it still takes an infinite amount of money to produce an infinite quantity. This is why, among the simple possible decline patterns, it is the only one that cannot be excluded based on its logic.
See on www.strategosinc.com
April 24, 2014 @ 3:42 pm
Years ago, when I asked my Shingijutsu sensei about learning/experience curves, he hit me on the head and told me that was the wrong way to think. I said “I understand that. But why does it not appear in the Lean literature?” His answer: Goods have to be designed to target costs, not produced in quantity sufficient to lower costs. He thought it a useless construct, like economic order qualities and economies of scale, which resulted in waste, unevenness, and unreasonableness. That’s why it is absent in the Lean literature. Also, see http://www.bobemiliani.com/goodies/emiliani_eos_slides.pdf
April 25, 2014 @ 6:07 am
I think your sensei just had a closed mind, probably as a result of spending too much time in the 100-year old car industry, which is too far down the experience curve for its effects to make much difference. If you plot the prices charged for the Model T against cumulative volume from 1908 to 1927 on log-log paper, you do find a straight line, but the car industry was young then.
In my early days as an engineer in the semiconductor industry, my US employer got a contract to supply about 10,000 special chips over three years to a Japanese customer, who provided us with a schedule of prices they were willing to pay.
Out of curiosity, I plotted these prices against cumulative volume on a log-log sheet, and found that they were on a straight line, leaving no doubt that they were based on experience curve assumptions.
The learning curve, and then the experience curve, started out as some form of empirical law of nature, quantifying the intuition that the more you have already made of something, the better you are at making even more. But then, pricing based on it forces it to be true, which makes it less a law of nature than a consequence of how players in a supply network make decisions.
Later, in automotive, I found it striking that the supplier support deal usually is a commitment by the supplier to drop prices by 3%/year in exchange for free consulting from the customer. Cumulative volume appears nowhere in the calculation, and experience curve thinking is not applied. Again, it is not because the phenomenon is not there, but because the industry so mature that it is negligible.
I saw what you wrote about economies of scale, but it is not what the experience curve is about. The example above was about 10,000 chips over three years, which is tiny volume, compared to, for example, 6 million units/month in a typical memory factory. The effect of experience curves is actually most visible during new product introduction, when cumulative volume doubles in a matter of days, then weeks, then months,…
April 25, 2014 @ 3:54 pm
Sorry; I should have mentioned the context. It was low volume production (high hundreds to a few thousand) of advanced military gas turbine engines. Instead of designing to a target cost, the designers largely ignored cost, leaving cost reduction to be achieved mainly through increases in volume (because they were so far from where costs needed to be, kaizen was not going to do it). The finance organization based projected costs on learning/experience curves. The customer found this to be acceptable, and paid the price in more ways than dollars. Anyway, the organizational dysfunction that ensued for nearly two decades, including many people replaced for failing to meet cost goals, was remarkable.
Having been in the line of fire when it comes to learning/experience curves, I can say that my sensei was absolutely correct. Learning curves, experience curves, economies of scale all drive people to accept the same misleading, simplistic cost-volume relationship, suggesting that all you have to do to lower costs is to produce more – overproduce, if needed. I consider it a dumb way to run a business. Cost problems must be addressed at the start of the process (design) and throughout, rather than mostly at the end of the process (production).
April 26, 2014 @ 4:13 pm
Quarterman’s article does not suggest that just making more of the stuff will make you go down the experience curve. In the semiconductor industry, you expect market prices to go down according to an experience curve, and whether these prices allow your company to hold a share of the market profitably depends on what your engineering and manufacturing organization does.
As most of the technical information is available only at the end of the process, when the chips are tested, the main motivation to reduce production lead times is to speed up learning. If it takes three months to complete the process, whatever you learn about its first operation is three months late. If you can do it in six weeks, it is more relevant.
Again, learning and experience curves are one thing, economies of scale another.
April 27, 2014 @ 6:02 am
Every finance person (and nearly every design engineer) I know thinks producing more will make you go down the experience curve. Michel, looks like we’re going to have to get Bill Waddell in on this conversation. 🙂