Jan 13 2011
Lead times, work sampling, and Little’s Law
On 1/11/2011, Michael Thelen asked in the NWLEAN forum about “laws of nature” as they related to Lean. This is based on one of my answers.
Lead time is a key performance indicator of manufacturing operations, but how do you measure it? It is not a quantity that you can directly observe by walking through a plant. To measure it directly you need to retrieve start and finish timestamps from historical data, assuming they are available and accurate. Or you could put tracers on a sample of parts, which means that it would take you at least six weeks to measure a six-week lead time. In most plants, however, a quick and rough estimate is more useful than a precise one that takes extensive time and effort to achieve.
That is where work sampling and Little’s Law come in handy. The key idea of work sampling, which the Wikipedia article fails to make clear, is that lets you infer a breakdown of each entity’s status over time from snapshots of the status of multiple identical entities. If, every time you go to the shop floor, you see 2 out of 10 operators walking the aisle, you infer that, on the average, each operator spends 20% of the time walking the aisle.
There are obviously necessary conditions for such an inference to be valid. For example, you want to take snapshots during normal operations, not during startup orshutdown, and the group you are measuring must be homogeneous: if it is comprised of two materials handlers and eight production operators, the 20% average is not interesting, even if it is accurate. Work sampling is usually described as applied to people, but the same logic is applicable to machines and to work pieces, and that is what makes it possible to infer lead times from snapshots of inventory and throughput rates.
On the shop floor, you can count parts, bins or pallets, and observe the pace at which they are being consumed. Let us assume we are in the context shown in Figure 1, and want to estimate how long we take to turn a blank into a finished good.
Figure 1. Context of Little’s Law
Little’s Law, then, says that on the average, in steady state, within one process or process segment,
Inventory = Lead time X Throughput
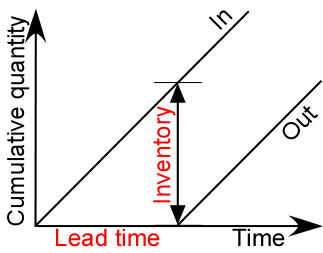
The reason this is true is best explained graphically, as in Figure 2, in the simple case of constant throughput and lead time. The cumulative count of blanks in is a straight line going up over time, and so is the count of finished goods out, offset by the lead time. The vertical distance between the curves is the number of blanks that have come in but not yet made it out as products, and represents therefore the inventory. The slope of each curve is the throughput, and it is clearly the ratio of the inventory to the lead time.
Figure 2. Little’s Law with constant throughput and lead time
What is interesting about Little’s Law is that it remains valid about averages when both rates of arrivals of blanks and departures of finished goods are allowed to fluctuate randomly about an average. This is probably the best known and most useful general result of queueing theory.
Since we can count inventory and measure throughput, we can infer average lead times from just this data. One snapshot will not give you an accurate estimate, but it is still considerably easier to take a few snapshots of a production line to get a more accurate estimate than it is to research history. The point is to get close to an answer that would take much longer to get if you actually had to be accurate.


Metrics in Lean – Part 5 – Lead times and inventory | Michel Baudin's Blog
July 11, 2012 @ 5:49 pm
[…] If the production rate and available stock fluctuate around the current levels, the item’s lead time from receiving into the warehouse through production will fluctuate around 20 days, by Little’s Law. […]
The staying power of bad metrics | Michel Baudin's Blog
November 21, 2014 @ 9:02 am
[…] The input data of the metric should be easy to collect. Lead time statistics, for example, require entry and exit timestamps by unit of production. The difference between these times then only gives you the lead time is calendar time, not in work time. The get lead times in work time, you then have to match the timestamps against the plant's work calendar. Lead time information, however, can be inferred from WIP and WIP age data, which can be collected by direct observation of WIP on the shop floor. Metrics of WIP, therefore, contain essentially the same information but are easier to calculate. (See Little's Law.) […]