How things are made.
Dec 23 2011
Via Scoop.it – lean manufacturing
The Manufacturing Digital ezine devotes an entire section to Lean, and this is the latest entry. It is more about what needs to be done than how to do it. In the featured picture, the executives look like the marines on Iwojima, but they also seem about to jump off a cliff.
Via www.manufacturingdigital.com
Nov 18 2011
Via Scoop.it – lean manufacturing
An important milestone in automotive manufacturing is taking place with Toyota’s celebrated Georgetown plant marking its 25th anniversary on Monday.
Via www.kentucky.com
Nov 1 2011
Via Scoop.it – lean manufacturing
For when you are not stuck with a 10-year old design…
Show original
Oct 26 2011
Data mining, in general, is the retrieval of information from data collected for a different purpose, such as using sales transaction histories to infer what products tend to be bought together. By contrast, design of experiments involves the collection of observations for the purpose of confirming or refuting hypotheses.
This perspective on data mining is consistent with the literature in expressing purpose, but most authors go further. They include in their definitions that data mining is done with computers, using large databases and specific analytical tools, which I think is too restrictive. The tools they list are the ones they have found useful in analyzing the behavior of millions of users of search engines or commerce websites, and they are not obviously applicable in other areas, such as manufacturing.
During World War II, British analysts used the serial numbers of captured or destroyed German tanks to estimate the numbers produced. Because serial numbers were not attached for this purpose, it was data mining. It used clever statistical models but, obviously, no computers.
Today, PhD-level data miners at Google, eBay, or Amazon sift through the page views and click-throughs of millions of users for clues to patterns they can use. The data, automatically collected, is accurate and collected by the terabytes every day. This “big data” requires parallel processing on clusters of computers and lends itself to the most advanced analytical tools ever developed.
Compared to this fire hose of data, what manufacturing produces is a trickle. In a factory, the master data/technical specs, plans and schedules, status of operations and work in process, and the history of production over, say, 12 months, usually adds up to a few gigabytes. It doesn’t fit on one spreadsheet, but it often does on a memory stick. On the other hand, much of it is still manually generated and therefore contains errors, and it is often structured in ways that make it difficult to work with.
Even if manufacturing companies could hire the data miners away from their current jobs, their experience with e-commerce or web search would not have prepared them well for the different challenges of manufacturing data mining.
There is an opportunity for data mining to contribute to competitiveness in manufacturing, but the approach must start from the needs. It must not be an e-commerce cure in search of manufacturing diseases.
Jan 13 2011
On 1/11/2011, Michael Thelen asked in the NWLEAN forum about “laws of nature” as they related to Lean. This is based on one of my answers.
Lead time is a key performance indicator of manufacturing operations, but how do you measure it? It is not a quantity that you can directly observe by walking through a plant. To measure it directly you need to retrieve start and finish timestamps from historical data, assuming they are available and accurate. Or you could put tracers on a sample of parts, which means that it would take you at least six weeks to measure a six-week lead time. In most plants, however, a quick and rough estimate is more useful than a precise one that takes extensive time and effort to achieve.
That is where work sampling and Little’s Law come in handy. The key idea of work sampling, which the Wikipedia article fails to make clear, is that lets you infer a breakdown of each entity’s status over time from snapshots of the status of multiple identical entities. If, every time you go to the shop floor, you see 2 out of 10 operators walking the aisle, you infer that, on the average, each operator spends 20% of the time walking the aisle.
There are obviously necessary conditions for such an inference to be valid. For example, you want to take snapshots during normal operations, not during startup orshutdown, and the group you are measuring must be homogeneous: if it is comprised of two materials handlers and eight production operators, the 20% average is not interesting, even if it is accurate. Work sampling is usually described as applied to people, but the same logic is applicable to machines and to work pieces, and that is what makes it possible to infer lead times from snapshots of inventory and throughput rates.
On the shop floor, you can count parts, bins or pallets, and observe the pace at which they are being consumed. Let us assume we are in the context shown in Figure 1, and want to estimate how long we take to turn a blank into a finished good.
Figure 1. Context of Little’s Law
Little’s Law, then, says that on the average, in steady state, within one process or process segment,
Inventory = Lead time X Throughput
The reason this is true is best explained graphically, as in Figure 2, in the simple case of constant throughput and lead time. The cumulative count of blanks in is a straight line going up over time, and so is the count of finished goods out, offset by the lead time. The vertical distance between the curves is the number of blanks that have come in but not yet made it out as products, and represents therefore the inventory. The slope of each curve is the throughput, and it is clearly the ratio of the inventory to the lead time.
Figure 2. Little’s Law with constant throughput and lead time
What is interesting about Little’s Law is that it remains valid about averages when both rates of arrivals of blanks and departures of finished goods are allowed to fluctuate randomly about an average. This is probably the best known and most useful general result of queueing theory.
Since we can count inventory and measure throughput, we can infer average lead times from just this data. One snapshot will not give you an accurate estimate, but it is still considerably easier to take a few snapshots of a production line to get a more accurate estimate than it is to research history. The point is to get close to an answer that would take much longer to get if you actually had to be accurate.
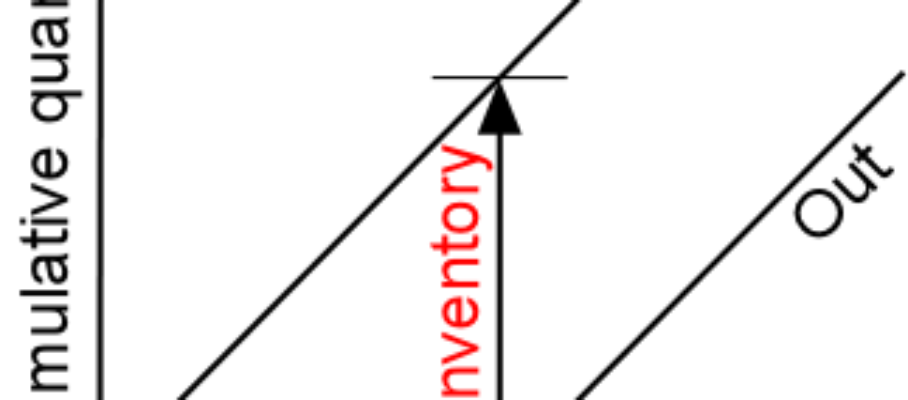
Feb 5 2012
Should Governments Subsidize Manufacturing Consultants?
Since 1988, the federal government of the United States has been subsidizing consulting firms through a program called Manufacturing Extension Partnership (MEP) out of the National Institute of Standards and Technology (NIST). The MEP has existed through five presidencies of both parties and now supports 1,300 consultants who provide cut-rate services to small and medium-size manufacturing companies, effectively shutting out other consultants from this market segment.
This raises the question of what qualifies an agency set up to calibrate measurement instruments to pick winners among consultants in areas like technology acceleration, supplier development, sustainability, workforce and continuous improvement. Clearly, the leaders of the MEP must have an extensive experience of manufacturing to make such calls.
Director Roger Kilmer just posted an article entitled A Blueprint for America: American Manufacturing on the NIST MEP blog. According to his official biography, the director of the MEP has been with NIST since 1974 and has never worked in manufacturing. On the same page, you can see that some members of the MEP management team have logged a few years in the private sector, in electric utilities, nuclear power, and IT services. None mention anything like 20 years in auto parts or frozen foods.
I agree with Roger Kilmer that manufacturing is essential to the growth of the U.S. economy, and even that government should help. All over the world, particularly at the local level, governments provide all sorts of incentives for companies to build plants in their jurisdiction. But is it proper for a government to directly subsidize service providers? The alternative is that whatever help is given go directly to manufacturing companies, for them to pay market rates for services from providers they choose.
In addition, the most effective help is not necessarily a subsidy. Hearing the CEO of a small, French manufacturing company uncharacteristically praise then finance minister Christine Lagarde, I asked what she had done to deserve it. “In 2009,” he said, “banks were denying credit to everybody. We were going bust. She decreed that bankers had to explain why for each case to her ministry. That was enough to pry the money loose.” It was done with a light touch, didn’t cost any money, and worked.
Share this:
Like this:
By Michel Baudin • Management • 3 • Tags: Government, Management, Manufactuting