May 20 2013
Orbit charts, and why you should use them
What I propose to call “Orbit Chart” is rarely used in manufacturing today, and I think it should be. This chart tracks the path followed by a system or an object in a plane where the coordinates are two of its characteristics. In earlier applications, there were geographical coordinates; in current ones, they may be the numerator and denominator of a financial ratio like Return On Net Assets (RONA), metrics of productivity and quality, or physical characteristics, like the depth and diameter of a drilled hole.
Most data visualizations in manufacturing are limited to simple charts, that show how one parameter varies by category, in bar graphs or continuously as a function of time in line plots. Charts that show more dimensions require more effort both to generate and to the read, but reveal information that you would not otherwise find.
Contents
- What is an “orbit chart”?
- Examples of orbit charts
- Minard’s Russia campaign chart
- Unplanned versus planned downtime in nuclear power plants
- GINI index versus GDP in Brazil and the US, 1980-2011
- Populations of predators and preys
- Parker Hannifin’s “North-by-Northwest” chart
- Orbit charts for spacecraft
- Recovery from crisis at Toyota versus GM
- Janet Yellen’s orbit chart of inflation versus unemployment
- Lora Cecere’s orbit charts of inventory turns versus operating margins for Colgate, P&G, Walmart, and Target
- How to generate orbit charts in Excel
- Orbit charts for multidimensional data
What is an “orbit chart”?
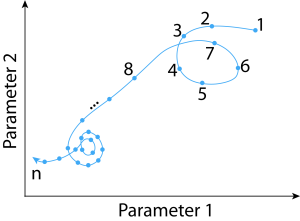
When you have an object moving in a plane, you can separately plot each coordinate against time, but the juxtaposition of the two plots would not show you the path followed in two dimensions. When you want to study a possible relationship between two parameters from a table of values where both are measured on the same objects, you usually start part generating a scatter plot, from which you try to infer some form of correlation between the two. When you do this, however, you lose the sequence information. When you consider two neighboring points on your scatter plot, you have no way to tell whether they are measurements on two units of product made consecutively or with many others in between.
On an orbit chart, you connect the points that succeed each other in the sequence, and label each point with its sequence number. As a result, what you plot is no longer a cloud of points, but a path followed by your object in the plane of your two parameters. On a road trip, the sequence of your locations at the end of each day are not independent: where you are tonight is where you were last night plus today’s increment. In machining with a tool that wears out, its condition after the 50th workpiece is what it was after the 49th, plus the effect of the 50th. The orbit chart is a visualization tool for this kind of phenomenon.
Let us assume that you are plotting the quality performance of a production line, as represented by its first-pass yield, against its productivity in terms of units/operator/shift. If you are practicing management whack-a-mole, you improve quality at the expense of productivity, by adding inspections and rework, or productivity at the expense of quality, by pressuring operators to cut corners. In this case, you can expect the orbit of your production line in the Quality versus Productivity plane to be a cycle, looking somewhat like a figure eight, and showing no real improvement.

On the other hand, if you are practicing Lean, quality and productivity improve together, resulting in a chart that does not loop.
Plotting an orbit, of course, is not always meaningful. In the following example, we show a scatterplot of two parameters measured on a sequence of independent events. The scatterplot lends itself to correlation and regression analysis of the two parameters, but tracing the path of the values in the sequence of points as on the right is meaningless.

Examples of orbit charts
The examples below are not from manufacturing but from military history, nuclear power plant maintenance, macro-economics, and ecosystems analysis. 25 years ago, radar charts were used in magazine like Britain’s The Economist, to compare parameters like inflation, unemployment and growth in multiple countries, but were unknown in factories, where they now are commonplace. Such may be the fate of orbit charts as well. The caveat is that, like radar charts, they are richer and more sophisticated than the usual charts you find on performance boards, and may be difficult for operators to relate to. As a result, they may be more useful as an analytical tools for engineers and managers than as a communication tool on the shop floor. The only way to find out is to try.
Minard’s Russia campaign chart
Perhaps the best known example of an orbit chart is Minard’s map showing the path of Napoleon’s army in 1812 Russia, on the offensive in brown, and retreating in black, with the thickness of the line showing the size of the army. It is annotated with dates, and with a temperature chart below. It was drawn in 1869, and Edward Tufte brought to the attention of readers in The Visual Display of Quantitative Information, as the most eloquent summary ever written about this disastrous campaign, and the mother of all infographics. Please click on the picture if you would like to enlarge it and read the text, knowing that it is in French. Tufte calls it a “narrative of space and time.” I prefer to call it “orbit chart” because (1) it is a shorter name and (2) the x and y coordinates do not necessarily represent space, nor is the index of the points always time. In manufacturing, for example, x and y could be quality characteristics, indexed by the serial numbers rather than time.
Tufte calls it a “narrative of space and time.” I prefer to call it “orbit chart” because (1) it is a shorter name and (2) the x and y coordinates do not necessarily represent space, nor is the index of the points always time. In manufacturing, for example, x and y could be quality characteristics, indexed by the serial numbers rather than time.
Unplanned versus planned downtime in nuclear power plants
I used the orbit chart below on p. 282 of Working with Machines, to compare the maintenance performance of the Japanese and French nuclear industries in the 1980s:
Jean-Pierre Mercier, from the French electrical utility EDF, published this chart to compare the evolution of nuclear reactor downtime in Japan and France. Each node on each of the orbits indicates performance in a given year, in terms of planned unavailability on the y-axis, and unplanned unavailability on the x-axis, and the sum of the two gives the total unavailability, so that diagonal lines indicate a constant total value. The orbits enable us to track year-by-year progress, and improvement is marked on the chart by movement towards the origin. The Japanese and the French orbits both show improvement over the years but are so different that they do not even intersect, which begs the question of why. What did the Japanese and French industries do so differently that it produced such radically different results? Once the chart prompts you to ask the question, it is easily answered:
- France has one national utility company, with reactors of just two designs all made by the same supplier. This company reduced downtime by redesigning components or subsystems that failed in one reactor, and retrofitting the changes to all sites of the same design.
- Japan has nine private utilities and reactors with many different designs, which made the French approach impossible. Instead, they overdid preventive maintenance in the beginning, and gradually improved it, eventually achieving almost the same performance as the French utility.
GINI index versus GDP in Brazil and the US, 1980-2011
This was back in 1990. Fast forward to 2013, and I am reading a new book by Alberto Cairo, called The Functional Art, about the design of information graphics and visualization. On p. XIX of the Introduction, I find the following chart of the orbit of Brazil’s economy in terms of GDP on the x-axis and the GINI index of inequality on the y-axis through five presidential administrations:  As explained on Wikipedia, the GINI index is a cleverly defined ratio, which is 0 if every member of a society has an equal share of its wealth, and 100 if it is all in the hands of a single individual. Worldwide, among the countries for which data is available, Sweden’s GINI index of 23 is the lowest, while South Africa and Lesotho have the highest, at 62. The US has gone from a low of 38 in the late 1940 to 47.7 in 2010. The GDP is a better known metric, and is here shown as evaluated in constant US$ by institutions external to Brazil, like the World Bank and the IMF.
As explained on Wikipedia, the GINI index is a cleverly defined ratio, which is 0 if every member of a society has an equal share of its wealth, and 100 if it is all in the hands of a single individual. Worldwide, among the countries for which data is available, Sweden’s GINI index of 23 is the lowest, while South Africa and Lesotho have the highest, at 62. The US has gone from a low of 38 in the late 1940 to 47.7 in 2010. The GDP is a better known metric, and is here shown as evaluated in constant US$ by institutions external to Brazil, like the World Bank and the IMF.
Assuming the underlying Brazilian economic statistics are credible, this chart tells quite a story, from the peak of inequality with low growth during hyperinflation under Sarney to sustained growth with steady reductions in inequality under Lula, the only pause in growth coming with the financial crisis of 2008. Would we see anything similar from plotting the same chart for the US economy? I tried, and the result is as follows:  What does this chart tell us? The first obvious conclusion are:
What does this chart tell us? The first obvious conclusion are:
- Regardless of economic circumstances or the political affiliation of the president, inequality has steadily increased in the US for over 30 years.
- We must always be wary of highly aggregated numbers. The US census bureau warns us that the formula for calculating the GINI index was changed for 1993, and that before-and-after comparisons are therefore not meaningful. On the face of the charts, it appears that even the high point of 47.7 for the US is lower than the low point of 53.8 for Brazil, but we would have to assume that the numbers are calculated the same way, which is doubtful. The formula was changed in the US; it may be different in Brazil and, unbeknownst to us, it may have been changed as well along the way.
- We can see, at the Bush(43)/Obama juncture, that the crisis of 2008 had a bigger impact on the US than on Brazil.
- While still roughly one sixth the size of the US economy, Brazil’s is growing faster. Back in 1980, it was less than one tenth.
Populations of predators and preys
For a long time, orbit charts have been used in population dynamics, with the x-axis being a prey population and the y-axis a predator population. Orbit charts can represent both theoretical models and actual data, when these are available. The following example, from a course taught at Portland State University, shows a simulation starting at the bottom right-hand side with a large prey population and few predators. This stimulates population growth for the predator, which depletes the prey population. This leads to a food shortage for the predators, causing their population to collapse, which in turn gives preys the opportunity to multiply again…

Eventually, the two populations spiral down not to a stable point, but to a repeating loop called limit cycle.
Parker Hannifin’s “North-by-Northwest” chart
Parker Hannifin is a diversified manufacturing company that included the following orbit chart is in its 2012 annual report:
Given the type of publication, the axes are unlabeled. Internally, this chart is also generated by division and monitored by General Managers. The black straight line represent constant RONA, and the desired movement is upwards and orthogonal to it, hence the nickname of “North-by-Northwest chart” given to it by managers. When it was first introduced a decade ago, it was not immediately understood, but it has taken root in the organization. I would connect the dots and annotate it as follows:
We can also see on this chart that, while the RONA improvements of 2010 and 2011 involved movement along both axes, in 2012, it was only a reduction in Net Assets/Sales, which is no doubt meaningful to someone familiar with the company’s operations.
Orbit charts for spacecraft
The term “orbit” of course is from astronomy, and I found a great example of an orbit chart drawn by NASA’s George Resteck of the path of the Pioneer 10 and 11 probes sent to explore the solar system in the early 1970s. As we can see on the chart, Pioneer 10 “only” managed to fly by Jupiter; Pioneer 11 flew by both Jupiter and Saturn, but crossed the other planets’ orbits far from where they were.

Only Voyager 2, launched 5 years later, managed to get close to all big four planets: Jupiter, Saturn, Uranus, and Neptune. The closest I could find to a similar chart for Voyagers 1 and 2 is as follows:
It is the same general idea, but with less details particularly on planet positions over time, and less information on scale. You can also find animations of their paths, but Resteck’s chart for Pioneer 10 and 11 still gives you the most information at a glance.
Recovery from crisis at Toyota versus GM
The following orbits of Toyota and GM profitability as a function of number of vehicles produced in recovery from crisis were included in a previous post:
The first shows GM through the growth of the twenties and the great depression; the second, Toyota through its 2001-2008 boom, followed by the financial crisis, the mass recalls of 2010, and the Fukushima earthquake and Thailand floods of 2011. It also shows how the economics of the auto industry changed in 80 years. In good times, today’s mature automobile industry yields profit margins that are barely 1/3 of what they used to be, on volumes that are many times higher. In the worst year of the great depression, 1932, GM made only 28% as many vehicles as in 1929. If the worst of the current crisis was in 2009-2010, Toyota’s drop in volume, while similar in absolute terms to GM’s in the great depression, was much smaller in relative terms, at barely 15% off from the 2008 peak.
The Toyota chart further shows three distinct periods:
- From 2001 to 2004, profit margins and volume rose together, suggesting that Toyota was enjoying some form of economies of scale.
- From 2004 to 2008, volume kept rising rapidly, but profit margins were flat. Toyota was criticized during that time for pursuing faster growth than it could manage.
- From 2008, the dominant effect is the financial crisis and recovery. with the 2010 recalls further reducing volume.
Janet Yellen’s orbit chart of inflation versus unemployment
David J (Joe) Armstrong pointed out to me an article from the New York Times on 10/9/2013 about Janet Yellen’s analysis of inflation and unemployment in the US since the Great Depression, using orbit charts and animations. The overall chart is as follows:
See the articles for animations and explanations of the different segments.
Lora Cecere’s orbit charts of inventory turns versus operating margins for Colgate, P&G, Walmart, and Target
David J (Joe) Armstrong also pointed out to me an article from Forbes Magazine on 12/13/2013 about supply chain collaboration, using orbit charts to show lack of progress. The charts are as follows:
Read the article for Lora Cecere’s analysis of the significance of these charts. My first question about them is whether these companies compute the plotted parameters in the same way. Only if we can be sure that they do, can we venture some conclusions from the charts. No units are given on the operating margin axis. Given that it is a ratio, I assume “0.06” means 6%.
The key point is that, in 12 years, none of these companies moved towards the best scenario of a high number of inventory turns and a high operating margin. In the case of Walmart versus Target, they seemed to have had “orthogonal” strategies, with Walmart moving up and down in inventory turns without any large gains in margin, while Target was moving back and forth in margin without major changes in inventory turns.
I think there are many factors that these charts don’t show, such as the impact of the competitive environment and the financial crisis. While neither manufacturers like P&G and Colgate nor retailers like Walmart or Target have shown much progress, the impact of inventory on their operations is quite different. Overall, the manufacturing companies buy materials and generate their margins from selling finished goods; they may have some items on consignment, but only a minority.
By contrast, if I understand how very large retailers work, their income does not come from markups on products but from the float in accounts payable. They pay suppliers a month or two after collecting revenues from selling to consumers, which adds up to a very large float, and the companies’ profits come from the income generated by this float in financial markets. In essence, their inventory is on consignment and their holding costs are nothing like the manufacturers’. They still have the costs of operating warehouses, but their own money is not tied up in materials paid upfront. On the other hand, their margins are sensitive to the health of the financial markets.
How to generate orbit charts in Excel
No matter how great orbit charts may be, not many people in manufacturing will use them unless they are easy to generate with Excel. Generating the orbit itself is not a problem. With Excel 2007 or 2010, all you have to do is, under the Insert tab, select Scatter and click one of the two options for Scatter with lines and markers. Then you can use the various formatting options to refine the axes, gridlines, etc. Most of the charts in this post were generated this way.

As you can see in the following example, Excel does not mind the curve looping and spiraling:

Labeling the points on the charts is trickier. If there are few enough, you can manually add text boxes on the chart, which is what I did, but it would not work for thousands of points. In fact, for any large number of points, your only options are:
- Labeling every n-th point.
- Making labels pop up next to a point when you hover on it or click on it.
The labeling option in Excel charts will display the numeric values for x and y or the name of the data series next to each point, which doesn’t tell you anything you don’t already know. You want to label each point with the value of its index in the data table so that, if it is time, you can know when each point was generated. Excel won’t do it, but Microsoft Support provides a Macro with which you can, with the result as follows:

In Alberto Cairo’s chart, the successive presidencies of Brazil were marked by a different color. In Excel, you could achieve this effect by have having a separate data series for each presidency, which you could then color as you wish.
Orbit charts for multidimensional data
Visualizing two dimensions of the evolution over time of a group of machines or the output of a production line is an improvement over plotting just one. But what if, instead of two, you have fifty or even ten characteristics of interest?
You cannot see a point with 10 coordinates, but you can use dimensionality reduction techniques to work around this problem. Principal Component Analysis, for example, projects these multidimensional points onto a plane so that the projections contain most of the variability of the full multidimensional cloud. Linda E. Kavraki provides the following illustration of the concept:

The coordinates on this plane are two uncorrelated linear combinations of the full set of coordinates called first and second principal components. Then you can plot the orbit of your population in this plane. Technically, it is straightforward, because you will easily find software packages to perform Principal Component Analysis. Minitab does it, and so does the XLSTAT add-in to Excel.
The challenge is making sense of the orbit chart. When you just plot the projection of your cloud of points onto the first two principal components, you may notice a small clump of points off to the side and identify them as outliers. But, when the points are generated over time, following the orbit may not tell you much because the coordinates are linear combinations of the original coordinates with no obvious meaning. The first principal component could well be three times the length of the ship minus half the captain’s age.









May 20, 2013 @ 5:37 pm
Comment on Linkedin:
May 20, 2013 @ 5:39 pm
I have seen this kind of chart in a variety of contexts without a generic name, and I thought they deserved one. I remember hearing the term “orbit” used in the same sense a few decades ago, to designate the path followed by solutions of differential equations. But, if you google “orbit chart,” the only items that come up are related to planets or electrons.
May 23, 2013 @ 4:11 am
Great article as usual, Mike. We have used these types of charting techniques to demonstrate convolutions and variation in process performance. Great visual charting techniques that help people to see what is going on in their processes.
May 23, 2013 @ 8:57 am
Comment in the Lean Six Sigma Worldwide discussion group on LinkedIn:
May 23, 2013 @ 6:36 pm
You are right that it is hardly a new idea, and its origins are in math, which is not a popular subject in manufacturing. My own introduction to this kind of plots was as a summer intern at the Hahn-Meitner Institut in Berlin in the summer of 1976, and it was memorable.
One of the doctoral students was trying to solve a system of equations governing the population of two types of defects in ionic crystals: interstitials — ions knocked out of position in the crystal lattice — and vacancies — the holes they leave behind. Of course, when an interstitial meets a vacancy, it falls into it and they cancel each other, which is the main factor of complexity. It is a bit like the population dynamics of single versus married men and women.
At the time, I often used translations of soviet textbooks, because they were cheap. In particular, I was fond of Vladimir Arnold’s treatise on ordinary differential equations, in which he showed how to plot orbits of the solutions of systems of equations on the back of an envelope when you can’t solve them analytically. I applied this technique to the doctoral student’s problem, which gave him the answer he was looking for. After that, we were able to plot a numerical solution, which was the first program I ever wrote, on a tiny Wang machine, in what I didn’t know was assembler.
Vladimir Arnold later taught at UC Berkeley and died in 2010. The doctoral student, now Dr. Wolf E. Montserrat, later worked on the recycling of spent nuclear fuels.
May 30, 2013 @ 6:42 am
Very useful. Thanks.
He’s just a numbers guy. | Consulting With Results
May 30, 2013 @ 12:49 pm
[…] Orbit charts, and why you should use them. […]
May 31, 2013 @ 8:56 am
Thanks a lot, I learned something today!
May 31, 2013 @ 11:02 am
Michel, thank you for the article. I see immediate applications for using orbit charts to help us visualize our data. The macro was easy to apply and very helpful. I look forward to your future posts.
June 1, 2013 @ 9:31 am
Very interesting. I have to see how this may be exploited in software engineering or business analysis or requirements engineering. Surely the shape and direction of paths reveal some “not easy to see” properties of the subject of study. I have added this to my favorites.
What’s Wrong With the Rote Application of Lean Tools? | Michel Baudin's Blog
August 25, 2015 @ 2:17 am
[…] contrast, a piece of software that generates orbit charts, for example, is much more similar to what we call a tool, because it draws instantly and […]
Orbit Charts, Revisited – Michel Baudin's Blog
September 23, 2023 @ 2:58 am
[…] Visualization Society journal, on 8/29/2023. What he called Connected Scatterplot is what I call orbit charts, and I have found them helpful, particularly in […]